BWL Mengenangaben (x) auf oder abrunden?
Wenn ich zwei Kostenfunktionen gleichsetze um eine Betriebsoptimalemenge zu berechnen, und diese liegt dann halt zb bei 512,21, runde ich dann auf oder ab? Man kann ja schlecht ,21 von etwas herstellen
2 Antworten
Im Allgemeinen sagt das nichtganzzahlige Optimum nichts über das ganzzahlige Optimum aus. Beispiel:
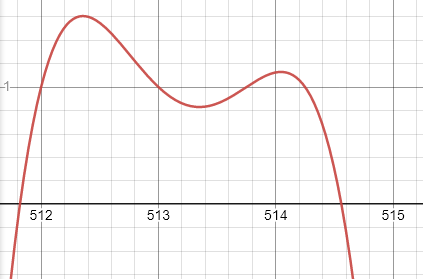
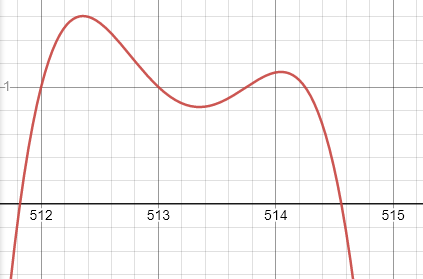
Hier liegt das globale Maximum zwischen 512 und 513. Aber der Wert bei 514 ist größer als der bei 512 und 513. Die ganzzahlige Optimierung ist ein wesentlich komplizierteres Problem. Wenn man wie bei quadratischen Funktionen dagegen weiß, dass es nur ein globales Extremum gibt, kommt dieser Fall nicht vor. Dann würde es reichen, 512 und 513 in die Funktion einzusetzen und zu vergleichen wo der bessere Wert rauskommt. Allgemein folgt auch nicht, dass die Zahl, die näher am nichtganzzahligen Optimum liegt, besser ist. Bei quadratischen Funktionen ist das aber auch wieder der Fall, da die Parabel achsensymmetrisch bezüglich der Senkrechten durch den Scheitelpunkt ist und sich die Funktion auf beiden Seiten genauso schnell verschlechtert.
Bei hohen Zahlen und allgemeinen ganzzahligen Optimierungsproblemen kann der Aufwand für die exakte Lösung größer sein als der Verlust durch Runden oder generell heuristische Methoden, mit denen man gute Werte bekommt, aber nicht unbedingt die besten, zumal das Modell die Realität auch nur vereinfacht darstellt und die Parameter geschätzt sind.
Man kann ja schlecht ,21 von etwas herstellen
Warum nicht? Wenn eine ME z.B. für Kubikmeter steht, wäre 0,21 m³ = 210 Liter
Bei Tonnen entsprechend 210 kg usw.
ME heißt ja nur Mengeneinheit, das muss nicht "Stück" bedeuten.
Das BO ist die Minimumstelle der Stückkostenfunktion.Genau genommen müsste man also den x-Wert nehmen, dessen y=k(x) das kleinste Ergebnis liefert. Das dürfte in den allermeisten Fällen der gerundete Wert sein.
Bei dieser ganzen Rechnerei sollte man die Realität nicht aus dem Auge verlieren. Als Kostenfunktion K(x) wird meist eine ertragsgesetzliche, also ganzrationale Funktion 3. Grades angenommen, die durch wenige Stichproben ermittelt wird. D.h. alles, was man aus dieser Annahme errechnet, ist mindestens genauso fehlerhaft bzw. geschätzt wie die Annahme.
Okay, hast recht, da hab ich mich falsch formuliert.
Wenns aber um Stück geht passt die Frage ja wieder, weisst du zufällig wie es dann abläuft?