Bitte nochmal Hilfe in Kombinatorik?
Seit Stunden, gestern und heute, versuche ich die Aufgaben in Permutationen, Variationen und Kombinationen zu sortieren, Ziehen mit oder ohne Zurücklegen, Reihenfolge wichtig oder unwichtig auseinanderzuklamüsern - und komme trotzdem mit den einfachsten Aufgaben nicht klar.
Z.B.: Ich habe vier verschiedene Getränke (Tee, Kaffee, Milch, Saft) und suche davon zwei Getränke aus. Wie viele Möglichkeiten gibt es für das Aussuchen der zwei Getränke?
Es ist eine Kombination ohne Zurücklegen und ohne Beachtung der Reihenfolge. Laut Formel ergeben sich 12 verschiedene Auswahlmöglichkeiten.
Aber wenn ich die Getränke ohne Formelberechnung notiere, ergeben sich nur 6 Auswahlmöglichkeiten: 3 (Tee mit Kaffee oder Milch oder Saft) + 2 (Kaffee mit Milch oder Saft) + 1 (Milch mit Saft).
Bin ich zu blöd für Kombinatorik? Bitte wenn möglich keine Zustimmung, sondern Trost und Ermutigung.
Euer entnervter Lumbricus
3 Antworten
Die 6 sind richtig. Ich weiß nicht welche Formel du verwendet hast, aber Kombination ohne wdh. wird berechnet durch den Binomialkoeffizienten ("n über k"). In diesem fall 4 über 2 = 6.
Hier auch nochmal die Formel für den Binomialkoeffizienten, falls du keinen Taschenrechner zur Hand hast:
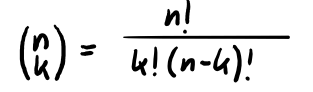
Ich hab dir hier mal einen einfachen Entscheidungsbaum gezeichnet:
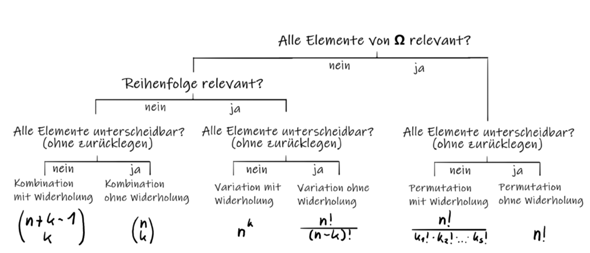
In deinem Fall, sind nicht alle Elemente der Grundmenge (gleichzeitig) relevant, also gehts nach links. Die Reihenfolge ist auch nicht relevant. Es gibt keine Wdh. also:
Kombi ohne Wdh.


Oh danke danke danke! :-) Jetzt fühle ich mich um mindestens 5 kg leichter. Die Kombinatorik hat mich richtig runtergezogen. Weißt Du, was mein Fehler war? Hab nicht richtig geguckt, hatte auf dem Bruchstrich 4 x 3 x 2 x 1 = 24, statt nur 4 x 3, hatte also auf dem Bruchstrich 4! und unter dem Bruchstrich 2!.
Die Formel in meinem Mathebuch ist aber auch komisch, ich versteh sie nicht, wenn ich sie auf die Getränkeaufgabe anwende:
K(n,k) = n x (n-1) x (n-2) x ..... x (n-k+1) auf dem Bruchstrich
1 x 2 x 3 x .... x k unter dem Bruchstrich
Daraus ist für mich nicht ersichtlich, dass ich (sh. Getränkebeispiel) auf dem Bruchstrich nicht die ganze 4!, sondern das nur zweimal ausführen darf, also 4 x 3.
Kannst Du mir vielleicht zeigen, woran ich an der Formel erkennen kann, dass ich (auf dem Bruchstrich) nicht 4x3x2x1, sondern nur 4 x 3 nehmen muss?
Und tausend Dank auch für den Entscheidungsbaum! Hab ihn schon ausgedruckt. Der ist verständlicher als der, den ich habe.
Bei Tee, Kaffee, Milch und Saft hast Du 4*3 Möglichkeiten, nacheinander zwei Getränke zu wählen.
Du könntest Tee und Kaffee wählen oder Kaffee und Tee. Du musst durch 2 teilen, wenn die Reihenfolge egal ist, also 4*3/2 =6.
Was ist dann, wenn es für eine Aufgabe nichts in der Formelsammlung gibt?
Ist dann die Fähigkeit, die Formel aus der Aufgabe abzuleiten, nicht wichtiger, als den Entscheidungsbaum gelernt zu haben?
Ja, das ist im allgemeinen wichtiger. Doch bei diesen Aufgaben blicke ich erst durch, wenn ich die Unterscheidungen intus habe. Wodurch unterscheiden sich Permutationen von Variationen, Variationen von Kombinationen? Dann kann ich mich an die Ableitung von Formeln machen. Wo ich noch Schwierigkeiten habe: Ich sehe noch nicht klar und deutlich, ob eine Reihenfolge da ist bzw. wichtig ist. Das bringt erst die Übung.
Aber gut, ich würde gerne die Herleitung der Formel des Binomialkoeffizienten verstehen. Hab es eben versucht, aber komme nicht drauf. Hast Du Lust, würdest Du mir einen Tipp geben? Also den Anfang vom Faden bräuchte ich.
4! / k! (n-k)! = 24 / 4 = 6
Machen wir mal mit 3 aus 6 also k aus n:
6*5*4 Möglichkeiten gibt es, 3 verschiedene Getränke zu wählen. Beim ersten sind es noch 6, beim zweiten 5 (das bereits Gewählte ist nicht mehr verfügbar), dann 4. Da spielt die Reihenfolge aber eine Rolle (Variation).
6*5*4 ist dasselbe wie 6!/3! in Variablen n!/(n-k)!
Wenn die Reihenfolge eine Rolle spielt, muss ich das noch durch k! teilen, denn immer 3! Variationen lassen sich zu einer Kombination zusammenfassen
Danke für deine Antwort. Den ersten Absatz verstehe ich glasklar.
Was ich noch nicht verstehe: Wo da die Reihenfolge ist. Meinst du das: Zuerst sind es 6, dann noch 5, und dann nur noch 4. Wenn eine Anzahl vermindert wird (oder vergrößert), dann nennt man es eine Reihenfolge? Also so versteh ich das: das eine sind Reihenfolgen von Objekten, wie sie dastehen, das andere sind Reihenfolgen von Tätigkeiten. Bin schon ganz konfus. Und was sind die Konsequenzen, wenn eine Reihenfolge da ist oder nicht, ich meine, was bewirkt die?
Du bist zu der Lösung n!/(n-k)! gekommen, = 720/6 = 120. Und die Formel ist die von einer Variation ohne Wiederholung.
Laut AltFVier ist es eine Kombination ohne Wiederholung, und das Ergebnis = 720/6x6 = 20.
Ich blick nicht durch! :-(
Eine Variation mit Wiederholung wäre, wenn Du Dir z.B. 3 mal hintereinander Bier auswählen dürftest.
Dann gäbe es 6^3 Variationen.
Ohne Wiederholung darfst Du das Getränk nicht nochmals nehmen, daher 6*5*4 Variationen, denn beim zweiten mal hast Du nur noch 5 Getränke zur Wahl usw.
Die Reihenfolge kannst Du wörtlich nehmen. Stell Dir vor, Du darfst alles gleichzeitig nehmen, dann spielt die Reihenfolge ja auch keine Rolle.
Bei der Kombination Tee, Kaffee und Milch (TKM) sind 6 Variationen vom Endergebnis her gleich.
Nacheinander TKM, TMK, KTM, KMT, MTK, MKT
Es gibt also diese k!=6 Variationen, die zum gleichen Ergebnis (hier:
Kombination) führen. Bei einer Kombination ist die Reihenfolge ja egal.
Da immer jeweils k!=6 Variationen zur gleichen Kombination führen, musst Du nochmals durch 6 teilen.
720/(6*6) ist also korrekt,.
Das mag für dieses Beispiel gelten, ist aber nicht universell anwendbar. Richtig ist es, den Binomialkoeffizienten zu verwenden.
Ich weiß nicht, ob das didaktisch gut ist. Ich plädiere immer dafür, erst eine Aufgabe von einfach bis komplex ohne Hilfe von Formeln zu verstehen.
Die 6*5*4 Möglichkeiten in beliebiger Abfolge lassen sich gruppieren in 3*2 prinzipiell gleiche Lösungen, müssen also dadurch geteilt werden.
Und das 6*5*4/(3*2) = 6!/3!/3! ist, ist nur eine universellere Schreibweise.
Noch schöner dann 6 über 3. Aber ich glaube, das kommt später dran.
Ich verstehe nicht, was du da machst.
Erste Auswahl: 4 Möglichkeiten, zweite Auswahl 3 Möglichkeiten: zusammen sind es 4*3=12 .
Ist doch ganz einfach.
Ich muss mich entschuldigen. Ich hatte dieses "ohne Beachtung der Reihenfolge" übersehen.
Du hast vollkommen recht. Deine Darstellung der Getränkekombination ist richtig. Die Formel ist "n über k" also diese grosse Klammer mit n oben und k unten. = n!/(k!*(n-k)! )= 4!/(2!*2!) = 2*3*4/(2*2)=6
Da ist sie, deine 6.
Nochmal sorry, meine Lösung war "mit Beachtung der Reihenfolge".
man kann seit Neuestem seine Antwort zeitlich unbegrenzt editieren !
eben nicht , du kannst jetzt morgen auch später noch editieren .
Ich meinte nicht "es ist jetzt zu spät" (zum Editieren) sondern: es ist schon nach Mitternacht, da habe ich mit dummem Kopf losgetippt und es richtig hingeschrieben ohne dran zu denken, dass ich den Fehler hätte ausmerzen können.
Das mit dem "dummen Kopf" wird dich jetzt freuen ....
Im Textkästchen rechts oben auf die Pünktchen gehen und dann auf "Antwort bearbeiten" klicken.
Das stimmt so nicht! Du verwendest hier die Formel für Variation ohne Wdh. Da hier die Reihenfolge aber KEINE Rolle spielt, ist das Ergebnis falsch. Auch wenn du für kleine Kombinationsmengen eventuell noch drauf kommen würdest, das Ergebnis durch 2 zu teilen, ist die Vorangehensweise für große Mengen falsch.
Ja, ist einfach, aber erst wenn man Durchblick hat. Ich bin nur noch soooo froh um das GuteFrage-Forum, dass ich Euch alle fragen kann, und nicht so hoffnungslos alleine rummurksen muss. :-)
Aber beachte, meine "ist doch einfach"-Antwort war falsch. Ich habe es drunter korrigiert.
Dein Vorschlag und deine Rummurkserei war völlig korrekt.
Ja, ich hab Deine Ausbesserung gelesen. :-)
Ja, das Prinzip hab ich eigentlich schon verstanden. Aber wenn es große Zahlen sind, versagt die Vorstellungskraft und ich muss mit den Formeln klarkommen, die ich nicht so gut verstehe.