Beweis/ Herleitung von Kreis-Flächeninhaltsformel: 1/2• b•r anhand dieser beiden Formeln (wenn möglich ausführlich):?
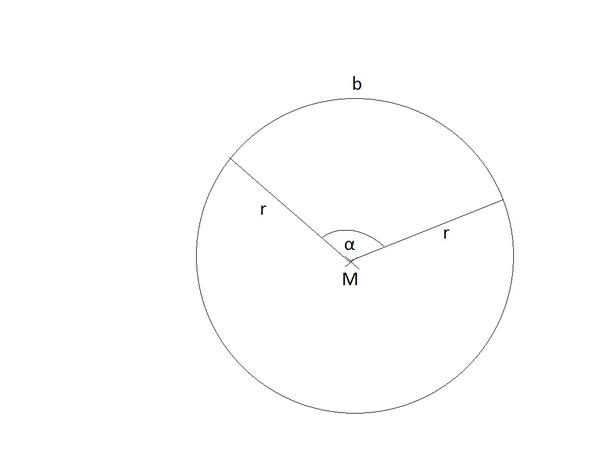
- Kreisbogen: b= 2• π• r• α/360° bzw. ...= π• r• α/180°
- A des Kreisausschnittes: A= π• r²• α/360°
Die ersten beiden Formeln verstehe ich gut und kenne deren Herleitung sowohl rechnerisch als auch zeichnerisch, jedoch weiß ich nicht weiter, wie ich diese beiden Formeln irgendwie gleichstellen soll, damit 1/2• b•r herauskommt. Kann mir da jemand helfen? Am besten wäre ein schrittweiser Rechenweg.
Danke im Voraus für Eure Mühe!
2 Antworten
Mit b = 2 • π • r • α/360° folgt: 1/2 • b = π • r • α/360°.
Also: A = π • r² • α/360° = (π • r • α/360°) • r = 1/2 • b • r...
Vielen Dank, das macht wirklich Sinn. Man muss also schauen, was beide Gleichungen gleich haben (in dem Fall also π • r • α/360°) und dann bei b geteilt durch 2 und bei A das eine r rausholen! Dafür gibts morgen den Stern ;)
Bevor ich eben meine Antwort abgeschickt habe, habe ich nochmal geschaut, ob bereits eine Antwort da war. Es war keine da.
Dann habe ich meine Antwort losgeschickt.
Jetz sehe ich, dass Deine Antwort schon 10min alt ist.
Frage: Werden Antworten erst mit Zeitverzögerung ins Netz gestellt?
fragender Gruß vom Geographen
b = 4 * pi * r * alpha / 360 = 4 * pi * (r * alpha/360)
(r * alpha7360) = b / (4 * pi)
A = pi * r^2 * alpha / 360 = pi * r * (r * alpha / 360)
A = pi * r * ( b / (4 * pi)) = 1/2 * r * b
Gruß vom Geographen
Wo holst du denn die 4 plötzlich her?
Trotzdem danke für den ausführlichen Weg, wobei mir die Erklärung von Melvissimo mehr zusagt!