Berechnung eines Flaschenzuges?
Hallo,
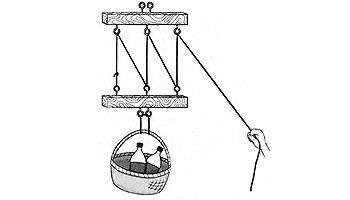
ich überlege die ganze Zeit wie ich den folgenden Flaschenzug berechnen kann.
Kann mir da jemand von euch helfen, wie ich an die folgenden Größen komme:
n: Anzahl der "tragenden Seile"
Fz: Betrag der Kraft, mit der man am Seil ziehen muss
3 Antworten
Die Anzahl der tragenden Seile ist 5, also alle bis auf der Teil, an dem man zieht. Da dient die obere feste Rolle nur zur Umlenkung der Zugkraft. Damit ergibt sich:
Fz = Fg / 5
Wenn das Seil oben fest gemacht ist, ist die Anzahl der tragenden Seile immer Anzahl lose Rollen * 2.
Wenn allerdings das andere Ende selber an einer losen Rolle oder am aufwärts gezogenen Gewicht befestigt ist, kommt immer gegenüber oben + 1 dazu.
Im Prinzip und praktisch gedacht, hast du recht. Die Last würde sich so leicht nach links verschieben, sodass die losen Rollen jeweils zwischen den festen liegen (horizontal gesehen). Aber das Bild ist nun mal so, wie es ist und das soll beurteilt werden. Womöglich gibts ja eine unsichtbare Führung, z.B. eine Gleitschiene links der Last oder eine Querseil nach rechts, das die Last in dieser Position hält.
Aber das Bild ist nun mal so, wie es ist und das soll beurteilt werden. Womöglich gibts ja eine unsichtbare Führung,
Das ist reine Spekulation und entspricht nicht "dem Bild wie es ist". Außerdem wäre die Seilzugkraft auch dann größer als Fg/5 (da denk mal nach !) und wird immer größer, je höher die Last gezogen wird.
Ich überlasse es jetzt deiner Intelligenz - und deinem Willen ! - Erkenntnis zu erlangen - mit Spekulation geht das eben nicht.
Also gerade habe ich bei Leifi Physik das hier gefunden: https://www.leifiphysik.de/mechanik/einfache-maschinen
Dort ist genau der Flaschenzug abgebildet.
Ich komme auf Fz = 1/n * Flast = 1/6 * Flast
Stimmt das?
Nein, das stimmt nicht. Du hast bei dem verlinkten Bild insgesamt 3 lose Rollen und 6 tragende Seile. Und da das Seil oben festgemacht ist, gilt: Anzahl der tragenden Seile = 2 * Anzahl der losen Rollen.
In der Aufgabe hast du aber nur 2 lose Rollen und das Seil ist unten an der Last festgemacht.
und das seil wird oben festgemacht, also genau wie es auf Leifi Physik abgebildet ist - sorry
Im verlinkten Bild ist das 2. Ende des Seiles oben an der Decke befestigt, während es im Bild in der Aufgabe nicht oben sondern unten an der Last befestigt ist.
@Hamburger02 wenn ich das Seil also nun oben befestige stimmt 1/6 ?
Also wenn du im Bild der Aufgabe das Seil an der linken der 3 oberen Rollen festbinden würdest, hättest du nur noch 4 tragende Seile, da das 5. ganz links entfallen würde.
Dann würde wieder gelten: Anzahl der tragenden Seile = 2 * Anzahl der losen Rollen.
Im verlinkten Bild auf leifphysik hast du 3 lose Rollen und 6 tragende Seile.
Okay jetzt habe ich das ganze verstanden. Vielen Dank!
Da ist man mit dem Bauingenieur Studium fast fertig, aber der Freundin einen Flaschenzug berechnen kann man nicht :) ;)
lol, sowas kenne ich. Nicht umsonst war bei uns im Studium ein geflügeltes Wort: "Is ja n'Ding. Gestern konnte ich Inschenör noch nicht schreiben und morgen bin ich schon einer."
Die Geometrie des Seilzuges kann sich unter Last so nicht einstellen.
Alle Seilabschnitte bekommen Schräglage bzw. der untere (obere ? Befestigung ?) Balken stellt sich schräg.
Die hier gemachten Angaben, die Seilkraft einfach als 1/5 der Last zu sehen ist wohl nicht zutreffend.
Ergänzung und Lösung
Wenn wir davon ausgehen - wie hier schon angedeutet - daß die Geometrie des Systems durch irgendwelche Führungsvorrichtungen erhalten bleibt, also sich weder verdrehen noch horizontal verschieben kann, dann ist
Fz= FL/(summe cos(a))
Fz=Seilkraft
FL= Lastkraft
a = jeweils der Winkel der hängenden Seile zur Senkrechten.
Beispiel hier mit der gegebenen Geometrie und Anzahl der Hängeseile
FL=1000N
a = 30°
Fz=1000/(3*1+2*0,866)=211,3N
Dies bedeutet, daß je nach Höhenlage, theoretisch , hier die Seilzugkraft zwischen FL/5 und FL/3 möglich ist.
n = zähl doch mal die Stricke, an denen nicht gezogen wird.
F = Last durch n
https://www.frustfrei-lernen.de/mechanik/flaschenzug-lose-feste-rollen.html
Denk nochmal darüber nach.
s. meine Antwort - oder irre ich mich hier ???