Aussagen über Ableitungsfunktionen?
Hallo Leute,
ich habe die folgende Aufgabe in der Mathearbeit nicht verstanden (ich habe sie heute wiederbekommen):
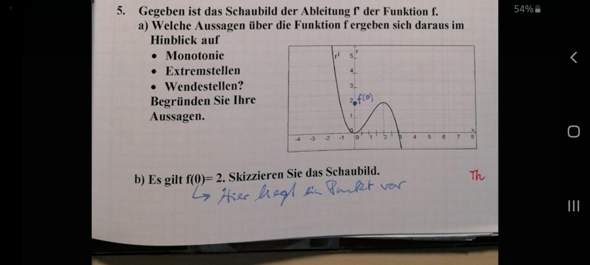
Welche Aussagen kann man über die Monotonie, die Extremstellen und Wendestellen der Funktion f treffen? Und b) verstehe ich irgendwie auch nicht, was genau muss ich dort machen?
2 Antworten
Aussagen
- Aus der doppelten Nullstelle von f'(x) bei x=0 ergibt sich ein Sattelpunkt von f(x)
- Aus dem Maximum von f'(x) ergibt sich ein Wendepunkt der Funktion f(x) bei x=2
- Aus der Nullstelle bei x=3 folgt ein Extremwert und aus dem Vorzeichenwechsel von Plus nach Minus folgt, dass es sich um einen Hochpunkt handelt
- Aus den positiven Werten im Intervall ]-∞; 3] folgt streng wachsende Monotonie und analog dazu, streng fallende Monotonie nach dem Hochpunkt.
Skizze
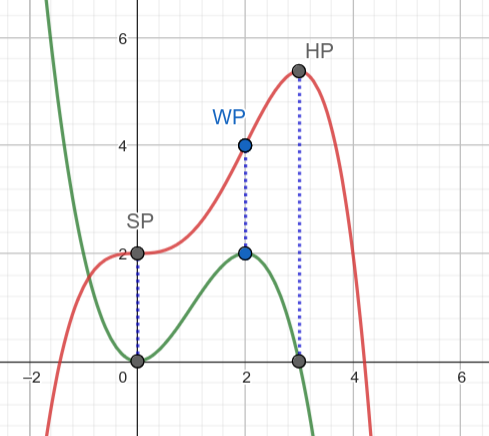
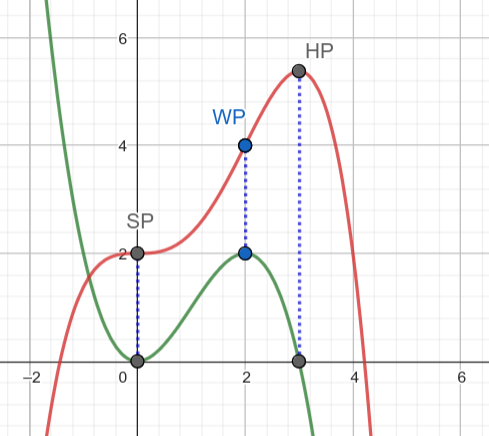
a) Monotonie: Wenn die Steigung einer Funktion in einem Bereich echt positiv ist (evtl. bis auf einzelne isolierte Punkte, an denen sie Null ist), dann ist sie in diesem Bereich streng monoton wachsend, das ist hier also von -unendlich bis 3 der Fall. Ab 3 ist die Steigung negativ, die Funktion also streng monoton fallend.
Du hast zwei Stellen an denen die Ableitung gleich Null ist - bei 0 und bei 3. Bei Null ist auch die Ableitung der Ableitung, also die zweite Ableitung gleich Null, also ist an der Stelle 0 ein Sattelpunkt. An der Stelle 3 ist die Ableitung gleich Null und die zweite Ableitung ist negativ, also hat die Funktion dort ein lokales Maximum.
b) da sollst du den Funktionsgraphen zeichnen.