Anwendungsaufgabe der Differentialrechnung in Mathe berechnen (Rühraufsatz Bohrmaschine U=30cm wie lang ist x/y)?
Für eine Bohrmaschine soll ein Rühraufsatz entworfen werden, der aus einem rechteckigen Metallrahmen mit 30cm Umfang besteht. Wie müssen Länge x und Breite y des Rechtecks gewählt werden, wenn beim Rühren ein maximales Volumen umschlossen werden soll.
Ich habe schon eine Hauptbedingung : A = x*y
Und eine Nebenbedingung : 2x+2y=30
Wie wird die Aufgabe weitergerechnet?

2 Antworten
Ich habe schon eine Hauptbedingung : A = x*y
Na ja, die Flächeinteressiert eigentlich niemaden. Da wird nach dem maximal umschlossenen Volumen gefragt...wenn das Teil rotiert.
Die Grundfläche A des enstehenden Rotationszylinders beträgt:
A = 2π * r = 2π * y/2 = π*y
Die Höhe des Rotationszylinders h beträgt x:
h = x
Und das Volumen V beträgt:
V = A * h = π * y * x
Nun lösen wir die Nebenbedingung nach x oder y auf, um es in V einsetzen zu können. Ich wähle y (weils praktischer ist):
2x+2y=30
y = (30 - 2x)/2 = 15 - x
also:
V = π * ( 15 - x) * x = -π*x^2 + 15π *x
Jetzt haben wir eine schöne Funktion:
V = f(x) = -π*x^2 + 15π *x
So sieht der Graph dazu aus:
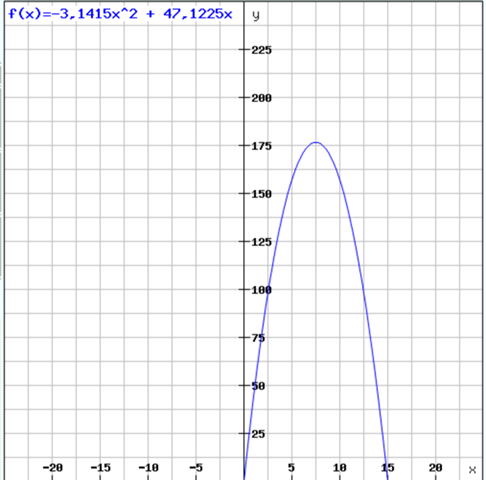
V soll maximal sein, also suchen wir den Hochpunkt von f(x):


Wir haben also ein Maximum bei x = 7,5 cm und das Volumen beträgt dann ca. 177 ccm.
Mit x = 7,5 cm folgt aus y = 15 - x:
y = 7,5 cm
Wir haben als Optimum ein Quadrat von 7,5 cm....was mich allerdings nicht sonderlich überrascht, da ein Quadrat bei gegebenen Umfang immer die größte Fläche hat und wenn das rotiert, hat es auch das maximale Volumen.


Schöne Antwort, nur leider ist sie falsch. Sie haben für den Flächeninhalt eines Kreises 2*π*r angeben, jedoch ist die Formel für den Flächeninhalt π*r^2, daher baut die die ganze Rechnung auf diesem Fehler auf. Der Nachweise meiner Behauptung liegt entweder darin, dass sie auf Google nachsuchen wie die Formel lautet, oder indem sie andere optionale Werte für x und y in das Volumen eines Zylinders einsetzten. Darauf werden sie herausfinden, dass das Volumen von 177ccm nicht maximal ist. Wir haben selbst im Mathematikunterricht diese Aufgabe zugeteilt bekommen, jedoch weiß ich selbst nicht genau, wie man diese mit dem richtigen Flächeninhalt löst.
Mfg
Ich bin jetzt nochmal alles durchgegangen und glaube, dass jetzt alles klar sein sollte.
Danke :)
Wieso interessiert die Fläche niemanden?
Die größte Fläche sollte doch auch das
größte Volumen umschließen.
Du löst die untere Gleichung nach y auf und setzt das oben ein.
Dann ableiten und Nullstelle der Ableitung berechnen.
Das ergibt x, y kannst du dann aus der unteren
Gleichung berechnen.