An die Mathematiker: wie löse ich das ohne irgendwelche Sätze o.ä.?
5 Antworten
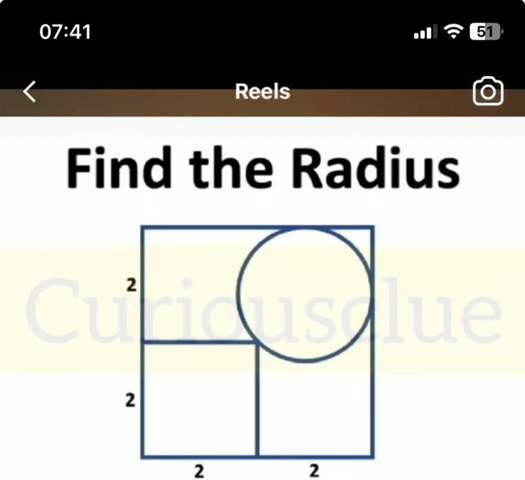
Rechter Berührpunkt des Kreises (4,a)
Oberer Berührpunkt des Kreises (b,4)
Berührpunkt des Kreises in der Mitte des Quadrats (2,2)
Aufgrund der Geometrie gilt a=b und der Mittelpunkt des Kreises liegt auf der Geraden y=x.
Daraus folgen die Gleichungen
(a-x)² + (4-x)² = r²
(2-x)² + (2-x)² = r²
Aus dem Gleichsetzen beider Gleichungen folgt
a = sqrt(x²-8), und für x = 4 damit a = sqrt(8)
Der Mittelpunkt (x,x) muss folgende Gleichungen erfüllen
(sqrt(8)-x)² + (4-x)² = r²
(2-x)² + (2-x)² = r²
Aus dem Gleichsetzen beider Gleichungen folgt
x = sqrt(8) und damit r = sqrt(8(3-sqrt(8)) ~ 1.1716
wie bist du nochmal auf:
(a-x)² + (4-x)² = r²
(2-x)² + (2-x)² = r²
gekommen, also ich habe mit der sqrt(8) weitergerechnet und komme auf das ergebenis, hab den abstand zwischen den beiden berührungspunkten berechnet und das ist die hypotenuse und der radius ist 2 mal die kathete, aber wie kommt man auf dieses gleichungssystem, was genau ist x?
Rechnung wie folgt.
Radius wäre 1,172
Ok ich gebe es zu. Ich habe es einen Video entnohmen. 😉
Nur hat der gute Mann italienisch gesprochen.
Konnte aber die Formel dann trotzdem erfassen.
Naja wurde ja inzwischen gut erklärt.
Ohne den Satz des Pythagoras gar nicht, denn der gibt dir die Länge der Diagonale des großen und des kleinen Quadrates.
Würde es mit einer Hypothenuse in einem rechtwinkligen Dreieck probieren. Die Werte Gast du ja schon.
Viel Erfolg ;-)
Vielleicht hilft dir ja das hier:
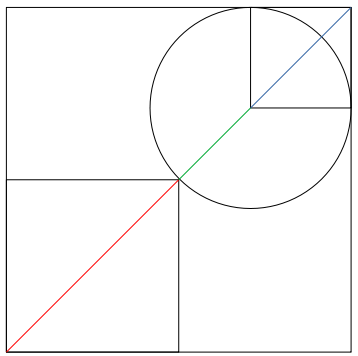
Ohne den Satz des Pythagoras (bzw. die Formel für die Diagonale eines Quadrates, die ja aus dem Satz des Pythagoras folgt) wird es nicht klappen.
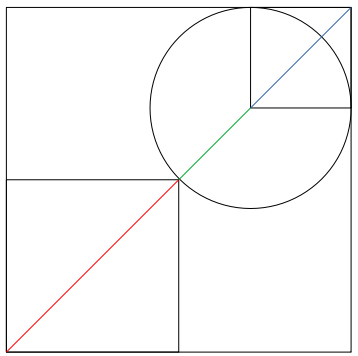
woher weißt du dass die hälfte der hälfte der diagonalen rechts oben genau die mitte des kreises darstellt? gibts da nen satz oder sowas?
Erstens ist das nicht die Hälfte der Diagonalen, und zweitens ergibt sich das aus der Anordnung des Kreises.
Dieser berührt die Seiten des äußeren Quadrates, daher sind die beiden schwarzen von mir hinzugefügten Linien jeweils gleich dem Radius des Kreises und treffen einander in dessen Mittelpunkt. Das obere kleine Quadrat hat also den Radius des Kreises als Seitenlänge, und die blaue Linie ist die Diagonale dieses Quadrates.
Die grüne Linie ist natürlich ebenfalls der Radius des Kreises.
naja die grüne linie ist der radius und die hälfte der hälfte der gesamten diagonalen, aber du hast das nur durch geometrie gezeigt, jedoch hast du dir das nicht korrekt mathematisch hergeleitet, das ist mir zu schwammig
Es handelt sich um eine geometrische Angabe, wie willlst du die Aufgabe ohne Geometrie lösen? Und dann auch noch ohne "Sätze"?
Meine Zeichnung sollte eine Hilfestellung sein.
Aus der Zeichnung folgt:
a·√2 + r + r·√2 = 2a·√2
Dabei ist a die gegebene Länge (a=2).
Obige Gleichung kann man nach r umstellen und somit r berechnen.
naja die grüne linie ist der radius und die hälfte der hälfte der gesamten diagonalen
Nein, sie ist nicht die Hälfte der Hälfte. Die blaue Linie ist länger als die grüne.
die treffen doch auf den mittelpunkt, aber dann hat man das gnaze trotzdem nicth gelöst
OK, ich gebe es auf. Ich kann dir aber versprechen, dass meine Lösung (die ich dir mittlerweile auch vorgerechnet habe) korrekt ist.
hmm ja stimmt safe, aber ist nicht so intuitiv, ohne Veranschaulichung hättest du es ja nicht rausgekriegt, und bei komplexeren Sachverhalten kann man das nicht immer so klar zeichnen
Klasse, aber wie kommt man darauf?