Additionstheoreme Beweisen?
Hallo,
wie kann man mit der Funktionalgleichung der Exponentialfunktion und den Formeln
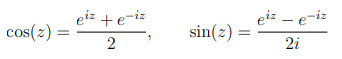
die Additionstheoreme für Sinus und Cosinus zeigen. (z und w sind Komplexe Zahlen)
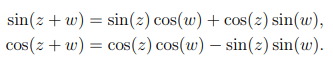
Meinst du mit Funktionalgleichung die Reihe, die exp definiert?
Wahrscheinlich ja, werde aus der Aufgabe auch nicht ganz schlau
1 Antwort
Hier ist es schnell erklärt.
https://youtu.be/aWwcHypoEg8?feature=shared
Hier kommen allerdings nicht direkt die Formeln aus den Bildern deiner Frage vor.
Du kannst einfach die Formeln für Sinus und Konsinus (also ihre Definition über die komplexwertige Exponentialfunktion) in die Additionstheoreme einsetzen und ausrechnen, sodass du am Ende zwei Gleichungen der Form 0 = 0 erhälst, also dass beide wahr sind.
Für den ersten Additionstheorem habe ich es dir vorgerechnet:
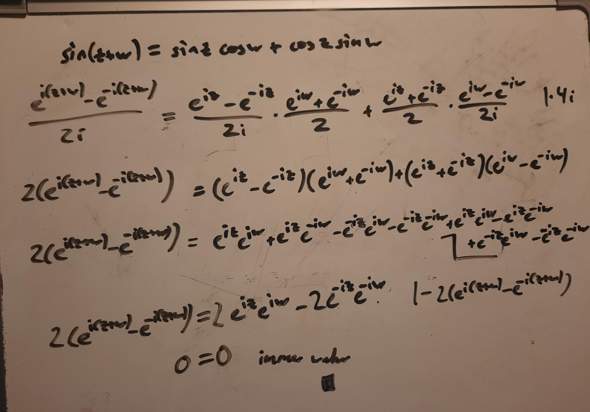
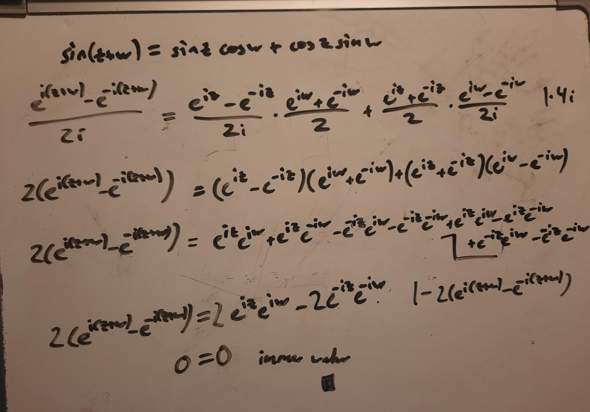
Ah ok, dann passt es.
Die habe ich in der vorletzten Gleichung indirekt angewandt (mit ihr ist gezeigt, dass auf beiden Seiten der vorletzten Gleichung das selbe steht).
Falls es dir weiterhilft:
Mit weiteren Zwischenschritten steht dort
2 (e^(i(v+w)) – e^(–i(v+w))) = 2 e^(iv) e^(iw) – 2 e^(–iv) e^(–iw)
2 (e^(i(v+w)) – e^(–i(v+w))) = 2 e^(iv+iw) – 2e^(–iv–iw)
2 (e^(i(v+w)) – e^(–i(v+w))) = 2 e^(i(v+w)) – 2e^(–i(v+w))
2 (e^(i(v+w)) – e^(–i(v+w))) = 2 (e^(i(v+w)) – e^(–i(v+w)))
Also auf beiden Seiten dasselbe.
Danke dir! Und mit Funktionalgleichung ist exp(a+b) = exp(a) * exp(b) gemeint