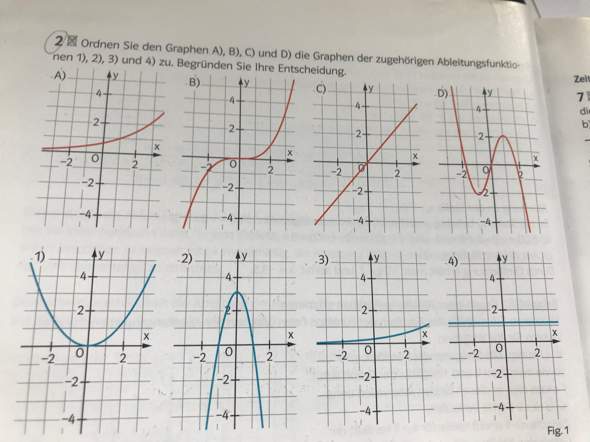
Ableitung grafisch was gehört zu was?
Ich würde das so zuordnen:
D-3
B-2
C-4
A-3
ist das so richtig und wie genau kann ich das gut begründen?
4 Antworten

Ich persönliche gehe immer nach dem NEW-Schema vor...da komme ich auf folgende Ergebnisse:
A3, B1, C4, D2
An hand von D läast sich das am besten erklären:
D hat bei -1/1 jeweils eine Extremstelle (E), darauf hin muss die Ableitungfunktion dort eine Nullstelle besitzen (siehe Bild), zum anderen hat D im Ursprung (P(0/0)) einen Wendepunkt, wodurch die Ableitungsfunktion dort eine Extremstelle haben muss, daraus schließt sich der Graph des 2. Bildes...
Nach dem Schema kannst du bei alles Zuordnungen vorgehen, funktioniert ganz gut, wenn man das einmal verstanden hat

Ich hab das auch nur aufgrund des ausschlussverfahrens ermitteln können, grundlegend würde ich aber sagen, da die Ausgangsfunktion weder Extremstelle noch wendestellen oder Hoch-/Tiefpunkte besitzt, kann die Ableitungsfunktion lediglich eine lineare Funktion darstellen...denn aus einer linearen Funktion kann nach ableiten keine ganzrationale funktion entstehen
1B 2D 3A und 4C
Merke:
1. Da wo die Ursprungsfunktion steigt, liegt die Ableitunhsfunktion oberhalb der x-Achse und da wo sie sinkt unterhalb
2. Nullstellen der Ursprungsfunktion = Hoch oder Tiefpunkt der Ableitungsfunktion
Wie genau bergründet man das bei 4C? Es heißt ja eigentlich wenn die Steigung von f null ist schneidet f' die Y-Achse?
Hi,
Ich hab est beim 3. mals Hinsehen, das eine Reihe aus a,b,c,d .... Inder unteren 1,2,3,4 Steht.
Die ersten Ableitung gibt die Steigung an. Die 2te Ableitung die Extrempunkte / Wendepunkte, Scheitelbunkte.
Ich gebe die mal 100 Punkte.
Mario
Richtig, das kannst du mit der steigung begründen
Wie genau bergründet man das bei 4C? Es heißt ja eigentlich wenn die Steigung von f null ist schneidet f' die Y-Achse?