Hey,
ich habe eine Digitaltechnikaufgabe bekommen, die mit Sicherheit nicht allzu schwer ist. Da mir das Modul nur wirklich gar nicht liegt muss ich euch um Hilfe fragen.
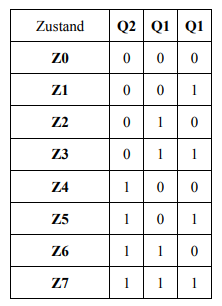
Ich habe folgende Tabelle gegeben:
Der Flipflop Q1 in der rechten Spalte ist ein Tippfehler und soll Q0 sein. Außerdem sind die Ausgänge der Zustandsflipflops gleichzeitig auch die Ausgänge.
Nun soll ich daraus das Zustandsdiagramm in Moore-Notation und Mealy-Struktur entwerfen -was ich gemacht habe - und in den weiteren Schritten Tabellen für die Folgezustände erstellen woraus ich dann die boolsche Gleichung ermitteln kann (für den späteren Schaltplan). Und genau hier hinkts. Ich habe keinerlei Angaben zu Zustandsübergangsbedingungen gegeben und auch keine Angaben zu Eingaben (welche ja sowieso für Mealy gut wären). Vielleicht hab ich auch einfach nur etwas übersehen und mir kann jemand helfen.
Schonmal vielen Dank im Voraus
Bei Fragen einfach fragen! :D