Wie kommt man auf das Termschemata für diese p-Zustände?
Atomarer Sauerstoff hat folgende Zustände in den 2p Orbits, wobei der linke der Grundzustand ist.
Die anderen beiden sind angeregte Zustände.
Nun verstehe ich nicht, wie man auf die Termbezeichnugen im Bild kommt:
bedeutet ja soweit ich weiß (?), dass die gesamte Drehimpulsquantenzahl L=1="P" ist und die 3 bedeutet die gesamte Spin-Multiplizität, d.h. in diesem Fall ist der Gesamtspin S=1
hat Drehimpulsquantenzahl L=2="D" und die 1 bedeutet die Spin-Multiplizität, d.h. in diesem Fall ist der Gesamtspin S=0
hat Drehimpulsquantenzahl L=0="S" und die 1 bedeutet die Spin-Multiplizität, d.h. in diesem Fall ist der Gesamtspin S=0
Frage: Wie kommt man nun darauf, dass Der Drehimpuls L im ersten Fall 1, im zweiten 2 und im dritten 0 ist?
Ich sehe hier kein System das ich anwenden könnte.
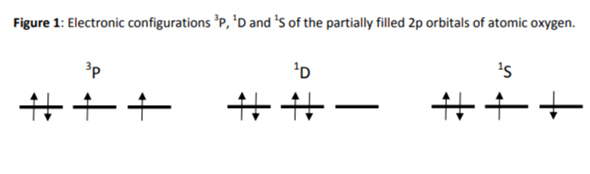
EDIT: Frage ergänzt (siehe Kommentar)
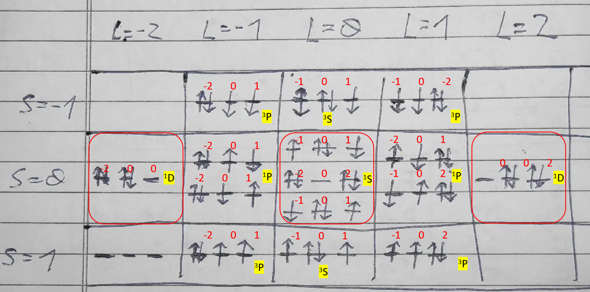
Ergänzung korrigiert. Das hier ist gültig, das vorige nicht.
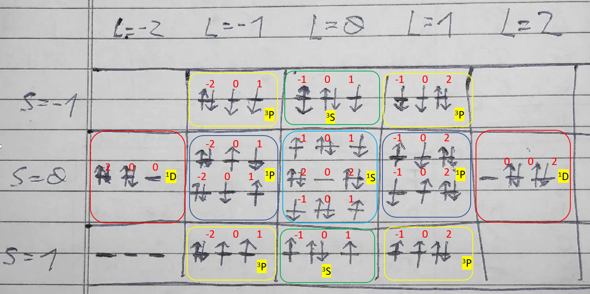
Der Anlass dieser Frage nachzugehen war eine Passage aus einem Vorlesungsskriptum über atomare Sauerstoffradikale, den ich nicht verstanden habe:

Ich wollte dies einfach verstehen und bin dann auf diesen Link gestoßen:
https://three.jsc.nasa.gov/articles/RadChemO2Sidebar.pdf
Seitdem sitze ich seit drei Tagen an diesem für mich unlösbaren Verständnisproblem.
1 Antwort
Du hast richtig beobachtet: Die Elektronenbesetzungen korrespondieren nicht wirklich zu den Termsymbolen. Das liegt im wesentlichen daran, daß Elektronenbesetzungen grundsätzlich Gurke sind. Quantenmechanik ist komplizierter als als nur Elektronen einfüllen.
Aus einer p⁴-Besetzung resultieren drei Zustände, ³P, ¹D und ¹S.
- Ein D-Zustand ist durch seinen Bahndrehimpuls fünffach entartet.
- Ein P-Zustand ist entsprechend dreifach entartet, und außerdem hat er als Triplett drei Spinkomponenten, also ist der ³P insgesamt neunfach entartet
- Der ¹S-Zustand ist dagegen überhaupt nicht entartet.
Die Zustände ¹D und ³P haben also mehrere Komponenten, und korrespondieren daher nicht zu einem einfachen Besetzungschema — das muß auch so sein, denn Atome sind kugelförmig, aber die einfachen Besetzungen sind das nicht (die Orbitale sehen ja irgendwie hantelförmig aus).
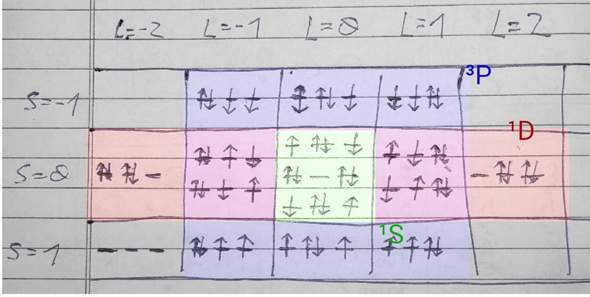
Wie man es richtig macht: Schreib alle möglichen Besetzungen auf. Du stellst fest, daß es genau 15 Möglichkeiten gibt, vier Elektronen in die drei p-Orbitale einzufüllen. Jedes p-Orbital hat natürlich einen der Werte m=−1,0,1, Du kannst also für jede Besetzung ein L=∑m ausrechnen. Ebenso kannst Du jeder Besetzung einen Gesamtspin zuordnen, indem Du einfach über die Spins summierst. Wenn Du das richtig machst, kommst Du zur folgenden Tabelle (ich habe dazu die p-Orbitale von links nach rechts mit m=−1,0,1 gezählt):

Nun zählst Du, wieviele Einträge jede Tabellenzelle hat und „zerlegst“ die Tabelle gedanklich in drei um den Mittelpunkt zentrierte Rechtecke. Das sieht dann so aus:
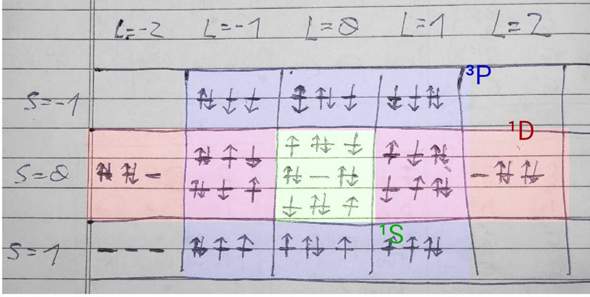
- Ein rotes 5×1-Rechteck in der Zeile S=0, das ist der ¹D — er ist fünffach entartet im Bahndrehimpuls, und nicht entartet im Spin
- Ein blaues 3×3-Rechteck, das ist der ³P. Er ist dreifach im Bahndrehimpuls entartet, auch nochmals dreifach im Spin.
- Dann bleibt noch die Zelle im Zentrum übrig (grün), die ist nicht entartet, also ¹S.
Die Zustände bestehen also aus 5 bzw. 9 bzw. 1 Komponenten (entsprechend den Tabellenzellen). Diese Komponenten geben die Entartung an, und sind ganz real; mit geeigneten Tricks, z.B. elektrischen oder magnetischen Feldern, kann diese Entartung ganz oder teilweise aufgehoben werden, und dann sieht man jede Komponente als unabhängige Zustände, mit Energieunterschieden und Übergängen und allem Drum und Dran.
Jede Komponente besteht aus Linearkombinationen von allen Besetzungen in der entsprechenden Zelle. Du siehst, daß es für den ³P und den ¹D Komponenten gibt, die nur aus einer einzigen Besetzung bestehen. Deshalb ist es möglich, unter Nachsicht aller Kuren und Taxen eine solche Besetzung zu anzuschreiben und damit den Zustand als ganzen halbherzig zu repräsentieren (obwohl es eigentlich nur eine einzelne Komponente davon ist).
Beim ¹S geht das aber nicht; seine einzige Komponente besteht aus einer Linearkombination von drei Besetzungen, und jede dieser Besetzungen trägt auch zu jedem anderen Zustand bei. Selbst mit zugedrückten Hühneraugen kann man daher den ¹S nicht durch eine einzige Besetzung semikorrekt repräsentieren. Wer das probiert (so wie der Verfasser Deines Skripts oder Lehrbuchs oder was auch immer), der muß kläglich scheitern, sobald jemand (so wie Du) genauer nachfragt.
Das ist vermutlich nicht die Antwort, die Du hören wolltest, aber die Quantenmechanik ist eben so wie sie ist. Wirklich einfach ist sie nur bei vollkommen besetzten Schalen.

Die Zustände sind die eingefärbten Flächen, nicht die Zellen. DIe Zustände haben möglicherweise mehrere Komponenten, aber jede Zelle ist für sich einmal gar nichts (außer der zentralen, die ist nämlich der einzige Beitrag zum ¹S).
Ich drehe nun durch...ich verstehe das Prinzip nicht: nehmen wir nur mal die Zelle mit L=0 und S=-1 her, also den mittleren Eintrag in der oberen Zeile: ich verstehe, warum hier L=0 und S=-1 ist, aber wieso gehört diese Konfiguration zu 3P? Hier ist doch L=0 und das würde ja einen S- Zustand bedeuten und keinen P...P Zustände haben immer L=1 oder L=-1 dachte ich...😰🥴
ich glaube, dass ich mich hier KOMPLETT verrantt habe, denn was du sagst, kann ich nicht mal ansatzweise nachvollziehen und ich weiß, dass du dich da auskennst.
Es ist meine Schlamperei, die Dich verwirrt: Ich hätte in der Graphik und auch in der Antwort Mₛ und Mₗ scheiben müssen.
Bei den p-Orbitalen wundert es Dich ja auch nicht, daß die mₗ-Quantenzahl drei Werte annehmen kann, nämlich mₗ=−1,0,1. Das p-Orbital hat zwar Bahndrehimpuls ℓ=1, aber eine der drei Komponenten hat trotzdem mₗ=0 — das ist kein Widerspruch.
(Orbitale sind einfach Zustande für ein einzelnen Elektron, daher sind die Regeln für die Kleinbuchstabenquantenzahlen ℓ,mₗ,s,mₛ dieselben wie für die Großbuchstabenquantenzahlen L,Mₗ,S,Mₛ, die sich auf mehrere Elektronen beziehen).
Es ist meine Schlamperei, die Dich verwirrt: Ich hätte Mₛ und Mₗ scheiben müssen.
Das war mir eigenlich klar. Nur verstehe ich nun nicht, wie eine Konfiguration aus der grünen Zelle gleichzeitig zu 1D und zu 1S gehören kann. Da gibt es ja eine Überlappung...genauso überlappen die violetten aus 3P mit 1D. Ich dachte wenn man eine Konfiguration hinschreibt, ist das bereits eindeutig ein S, P oder D Zutand. So wie du das beschreibst ist das aber nicht der Fall. Jetzt bricht eine Welt für mich zusammen...
Und dann verwirrt mich auch noch dies: schau mal wo der ganz linke 3P und der ganz rechte 1S Zustand aus meinem ganz ersten Bild in deinem Diagramm liegen. Der 3P Zustand ist bei dir links unten im blauen Feld der 3P Zustände, aber der 1S liegt bei dir bei L=-1 und S=0, also nicht im grünen mittleren Feld. Das passt ja alles hinten und vorne nicht zusammen...
Die mittlere Zelle enthält drei verschiedene Besetzungen. Daher gehört sie auch zu drei Zuständen — jede dieser drei Zustände hat ja eine Komponente, bei der sowohl Mₛ=0 als auch Mₗ=0. Es hat ja auch jedes Orbital, egal ob s,p,d,f,… eine Komponente mit mₗ=0.
Das ist ein bißchen überraschend, denn man stellt sich z.B. einen Triplett (S=1) so vor, als ob da immer zwei ungepaarte Elektronen vorhanden sind. Aber der Triplett hat drei Komponenten, und in einer davon ist Mₛ=0.
Jeder Zustand (=farbige Fläche) hat in jeder Tabellenzelle, die er abdeckt, eine Komponente — ja, der ³P hat auch eine Komponente für Mₛ=0 und Mₗ=0, obwohl S=1 und L=1.
Diese Komponenten sind irgendwelche häßlichen Linearkombinationen der betreffenden Elektronenbesetzungen, die zueinander orthogonal sind. Wenn eine Zelle nur zwei Besetzungen enthält, dann sind diese Linearkombinationen einfach nur Summe (für Triplett) und Differenz (für Singulett) der Besetzungen, bei dreien wird es häßlicher.
Deine Graphik verstehe ich nicht, und das liegt vermutlich daran, daß sie daneben ist. Schau Dir bitte meine eingefärbte an: Die drei farbigen Rechtecke (3×3, 1×5 und 1×1) sind die Zustände. Die Termsymbole ³P, ¹D und ¹S habe ich einfach in gleicher Farbe an irgendein Eck der Rechtecke dazugeschrieben, sie beziehen sich auf die Rechtecke mit dieser Farbe
(Die zentrale Tabellenzelle gehört zu allen drei, aber das kann man mit Farbe nicht ausdrücken; sie kann ja nicht gleichzeitig grün, rot und blau sein).
Aber dann kann man doch nicht eine 1:1 Relation zwischen einem Besetzungsbild (siehe mein erstes Bild) und einer Termbezeichnung machen: Wenn ich eine Besetzung aus deinem grünen Bereich im Zentrum nehme, wie kann ich dann sagen, dass diese entweder 1S oder 3P oder 1D ist? Laut deiner Beschreibung hehört sie ja zu allen gleichzeitig. Eine Zeichnung, die einer konkreten Besetzung eine eindeutige Trembezeichnung zuweist, wäre dann ja völliger Quatsch.
Deine Graphik verstehe ich nicht, und das liegt vermutlich daran, daß sie daneben ist.
welche meinst du? Meine Ergänzung wo ich in deine Tabelle die gelben Bezeichnungen dazugeschrieben habe oder die ganz erste, auf die sich meine Frage bezieht?
Ich habe meine Frage oben ergänzt, wo ich den Grund für meine Nachforschungen angegeben habe und woher das Bild stammt. Eigentlich dachte ich, das wäre in 5min erledigt - nun sitze ich seit Tagen daran und verstehe weniger als zuvor 😂😂😂
Ich werde mir mal deinen Link "The Russell Saunders Coupling Scheme" durchlesen. Mich macht es krank, wenn ich was nicht vertanden habe. Geht das etwa in Richtung Clebsch-Gordan Koeffizienten? Die habe ich schon im Studium nicht wirklich verinnerlicht, aber nun muss ich es scheinbar nachlernen, sonst verstehe ich das nie.
"ich weiß dass ich nicht weiß..." fällt mir hierzu nur ein.
🤣 Ich gehe jetzt mal schlafen. Aber gegessen ist das Thema noch nicht und ich melde mich gegebenenfalls wieder bei dir.
Ja, genau: Die Clebsch–Gordan-Koeffizienten sind die Koeffizienten, die die Elektronenbesetzungen zu den Komponenten der Wellenfunktion für die Mehrelektronenzustände linearkombinieren.
da muss ich nun nach mehr als 30 Jahren wieder meine Quantenmechanik Unterlagen auskramen -
Aber dann sind solche Besetzungsbilder doch völliger Quatsch. Wieso wird das dann immer wieder so gelehrt frage ich mich...???
Ich habe aus Quantenchemie dissertiert. Aber diese Frage kann ich wirklich nicht beantworten — ich habe absolut keine Ahnung.
wobei ich gerade nochmal nachgekramt habe: die Clebsch Gordan Koeffizienten sind für die Addition von zwei Drehimpulsen. Hier haben wir ja aber vier oder gar mehr. Kann man das überhaupt verwenden?
und warum haben dann der 3P und der 1S aus meinem ganz ersten Bild unterschiedliche Buchstaben, obwohl sie sich in den Besetzungen nur hinsichtlich der Spins unterscheiden? Was in diesem Bild mit 1S bezeichnet wird, hätte ich mit 1P bezeichnet. Bin ich jetzt ganz verrückt geworden???
Ganz offen gesagt habe ich es nicht verstanden, obwohl ich mich bemüht habe.
Ich beziehe mich hier auf meine aktuelle Ergänzung der Frage.
Es fängt schon mit der Termbezeichnung an: Was bedeutet
1D, 3P und 1S ?
Ich dachte dass
- die hochgestellte Zahl die Spin-Multiplizität angibt, das wäre dann in der zeile für S=0 die Zahl 1 und für die Zeilen mit S=+1 oder -1 die Zahl 3.
- der Buchstabe für den Bahndrehimpuls L steht, also S, P, D für L=0, 1, 2
Und so käme ich auf die gelb herbvorgehobenen Bezeichnungen in meinem ergänzten Bild. Hier hätte ich
- 2Konfigurationen mit 1D (5 fach entartet im Bahndrehimpuls)- rot
- 4Konfigurationen mit 3P (3 fach entartet im Spin, 3 fach entartet im Drehimpuls) - gelb
- 3Konfigurationen mit 1S (keine Entartung) - hellblau
- 4 Konfigurationen mit 1P (3 fach im drehimpuls entartet)- dunkelblau
- 2 Konfigurationen mit 3S (3 fach spin entartet,)
Die letzteren Termbezeichnungen kommen bei dir gar nicht vor - deshalb mache ich hier wohl etwas falsch: ich ordne den 3 Platzhaltern die Lm Komponenten -1, 0, 1 zu und addiere auf: Die Summen der roten Zahlen ergeben dann L=-2, -1, 0, 1, oder 2.
Jetzt kenne ich mich noch weniger aus als vorhin: warum habe ich hier 1P und 3S Zustände. Und wo siehst du da ein 5x1 Rechteck?
Ich gebe zu, daß ich schlampig war. In der Tabelle sollten statt den Quantenzahlen S und L deren Projektionen auf die Vorzugsachse stehen, also Mₛ und Mₗ (die Indices S und L sollten Großbuchstaben sein, aber das kriege ich hier leider nicht hin).
Grundsätzlich hast Du recht — die Multiplizität ist nur einer verklausulierte Angabe der Quantenzahl. Ein Zustand mit S=1 (Gesamtspin) hat Multiplizität 3 und heißt Triplett. Die Bezeichnung kommt daher, daß er aus drei Spinkomponenten besteht, und das hat man experimentell gesehen, noch bevor man wußte, was ein Spin ist. Man konnte also messen, daß aus dem einen Zustand im Magnetfeld plötzlich drei werden, und deshalb hat man es Triplett genannt.
Ich habe jetzt die Rechtecke im Schema farblich hervorgehoben.
- Das 3×3-Rechteck (also ein Quadrat, aber alle Quadrate sind ja auch Rechtecke) ist blau und deckt neun Felder ab, das ist der ³P — er hat drei mögliche Werte für die Spinorientierung Mₛ, und drei für die Bahndrehimpuls-Orientierung Mₗ.
- Das 1×5-Rechteck ist rot, es hat nur einen Wert für die Spinorientierung und fünf für den Bahndrehimpuls, also ¹D.
- Es verbleicht noch die Tabellenzelle im Zentrum, also ein 1×1-Rechteck, das zum ¹S gehört.
- Auf jeder Tabellenzelle liegen genau soviel Rechtecke, wie die Zelle einträge (Elektronenkonfigurationen) hat.
Ich hoffe, das wird jetzt etwas klarer. Wenn nicht, frag nach.
Wenn Du ein Elektron in ein s-Orbital setzt, dann ist mₛ=½ und die Multiplizität ist 2 (Dublett), der Zustand ist ²S (weil der Bahndrehimpuls Null ist, und Null heißt S). Ein Elektron in einem p-Orbital bildet entsprechend einen ²P-Zustand. Sobald mehr als ein Elektron im Spiel ist, brauchst Du das beschriebene Verfahren (Russel–Saunders-Kopplungsschema), um die Zustände aus der Besetzung herauszukitzeln. Du kannst es ja einmal selbst mit p³ oder d² oder so irgendetwas versuchen und mir schreiben, was Du herausbekommst.
Beim Bahndrehimpuls ist es im Prinzip gleich, auch da ist die Entartung 2L+1, aber da nennt man das nicht Multiplizität, sondern schreibt das L verklausuliert als Buchstabe direkt an. Ein Termbezeichnung wie ³D bedeutet also Gesamtspin S=1 und Gesamtdrehimpuls L=2.
- Was Spin S=1 hat, liegt in drei Komponenten vor, die mit einer Mₛ-Quantenzahl durchnumeriert werden.
- Was Bahndrehimpuls L=2 hat, liegt in fünf Komponenten vor, die mit einem Mₗ-Quantenzahl durchnumeriert werden. Das kennst Du im Prinzip von den Atomorbitalen, da haben wir nur ein Elektron und daher Kleinbuchstaben: ℓ=2 und mₗ=−2,−1,0,1,2; die Komponenten unterscheiden sich im wesentlichen in der Orientierung.
- Bei Mehrelektronensystemen nimmt man Großbuchstaben für den Gesamtspin bzw. den Gesamtdrehimpuls.
Du hast das eingefärbte Bild von dir: warum ist die Konfiguration in der Zeile mit S=-1 und L=0 ein 3P Zustand? L=0 wäre meiner Ansicht nach ein S- Zustand...