Zeitdilatation von Licht -> Licht bewegt sich nicht?
Hallo zusammen,
als physikalischer Laie zerbreche ich mir an einer Frage zuletzt den Kopf, da meine Schlussfolgerung einfach nur falsch sein muss. Leider habe ich dazu sonst nichts im Netz gefunden aber vielleicht kann hier ja jemand meinen Fehler in der Schlussfolgerung finden.
- Licht bewegt sich mit Lichtgeschwindigkeit
- Für bewegte Objekte vergeht deren Zeit langsamer
- Für bewegte Objekte die sich mit Lichtgeschwindigkeit bewegen bleibt die Zeit stehen
- Da Licht sich mit Lichtgeschwindigkeit bewegt vergeht für Licht keine Zeit
- Weil für Licht keine Zeit vergeht kann es sich auch nicht bewegen, da Geschwindigkeit Strecke/Zeit. Da keine Zeit vergeht und in dem Fall immer Null wäre bewegt es sich nicht?
Wo ist hier mein Denkfehler? :)
Gruß,
Christoph
3 Antworten
im limes v-->c (und nur so macht es sinn) geht die sowohl die eigenzeit als auch die die "proper length" (ich kenne keinen deutschen begriff dafür) gegen 0.
wenn ein teilchen die strecke mit länge s (gemessen im bezugssystem S) mit geschwindigkeit v (bezogen auf bezugssystem S) zurücklegt und dafür natürlich die zeit (gemessen im bezugssystem S) t=s/v benötigt, dann ist die während dieser reise für das teilchen vergangene eigenzeit gleiche t'=s*Wurzel[1-v²/c²]/v und die zurückgelegte strecke entspricht s'=s*Wurzel[1-v²/c²]
wenn du den limes v-->c nimmst siehst du dass sowohl t' als aus s' gegen 0 gehen.
die zurückgelegte strecke (aus sicht dieses teilchens) geht also in der tat gegen 0.
aber das heißt ja nicht dass es sich nicht bewegt, in jedem anderen bezugssystem ist ja die strecke größer als 0.
...dann ist die während dieser reise für das teilchen vergangene eigenzeit gleiche t'=s*Wurzel[1−v²/c²]/v ...
Soweit richtig. Ich würde vielleicht β = v⁄c einführen und
t' = (s⁄βc)∙√{1 − β²} =: (s⁄βc)/γ
schreiben.
...und die zurückgelegte strecke entspricht s'=s*Wurzel[1−v²/c²]
Von was zurückgelegt, muss man in diesem Fall fragen. Vom Teilchen selbst nämlich nicht, denn S' ist ja sein Ruhesystem.
Das ist immer der Riesenfehler, wenn man sagt "in S' muss das Teilchen nur die Strecke s∙√{1 − β²} zurücklegen" – nein! In S' bewegt sich nicht das Teilchen, sondern das Zielobjekt kommt mit βc auf das Teilchen zu und ist nur mehr
s' = s∙√{1 − β²} =: s⁄γ
entfernt. Hätte das Teilchen Augen und könnte Entfernungen bestimmen, würde es den Körper aber nicht in der Entfernung s', sondern in der Entfernung
s'⁄(1 − β) = s∙√{(1 + β)⁄(1 − β)} =: s∙K,
wobei K der BONDI- Faktor ist, der Faktor des optischen DOPPLER- Effekts (der sog. K- Kalkül erklärt die SRT viel konkreter, und es kommt einem nicht mehr so "magisch" vor).
Hallo Goschi2,
in Deiner Überlegung …
Weil für Licht keine Zeit vergeht kann es sich auch nicht bewegen, da Geschwindigkeit Strecke/Zeit.
… stecken zwei Denkfehler:
- Die Zeitspanne steht im Nenner. Wenn der 0 ist, ist der Quotient nicht definiert. "Sich nicht bewegen" bedeutet, dass ein Körper während einer endlichen Zeitspanne am selben Ort bleibt, also null Strecke zurücklegt. Hier ist das Gegenteil der Fall.
- Die Zeitspanne, die Du hier in den Nenner setzt, ist die Eigenzeit. Die Geschwindigkeit eines Körpers ist aber als Ortsverschiebung/ Koordinatenzeit definiert. Wie der Name sagt, ist das eine Koordinatendifferenz in einem bestimmten Koordinatensystem, das wir dabei als Bezugssystem benutzen.
Angenommen, A und B seien Stationen, die sich relativ zueinander nicht bewegen, also ein gemeinsames Ruhesystem Σ haben. Sie haben natürlich Borduhren, und die sind Σ- synchronisiert.
Du bewegst Dich von A nach B.
- Wenn Du bei A auf deren Uhr guckst und bei B auf deren, hast Du die Σ- Koordinatenzeit Δt = t₂ − t₁ ermittelt.
- Wenn Du bei A und B auf Deine eigene Uhr guckst, ist das eine direkte Messung der Zeitspanne Δτ = τ₂ − τ₁; dies ist die Eigenzeit.
Was zum Henker heißt "Σ- synchronisiert?" Nun, wir nehmen an, dass die Borduhr von B die Bezugsuhr ist und die Uhr von A mit ihr synchronisiert werden soll.
"Σ-" deshalb, weil wir in Σ rechnen, also A und B als stationär betrachten. Das impliziert die Annahme, dass Differenzgeschwindigkeit zwischen Signal und A bzw. B ebenfalls in beide Richtungen c beträgt.
Wenn man die Entfernung d kennt, programmiert man die Borduhr so, dass sie beim Empfang eines Signals mit einem bestimmten Zeitstempel t₀ automatisch d⁄c addiert, sich also auf t₀ + d⁄c stellt.
Wenn man d nicht genau genug kennt, schickt man ein Signal hin, das eine Antwort von B mit Zeitstempel auslöst, und bekommt die Antwort mit Zeitstempel t₀ eine Zeitspanne T nach Abschicken zurück. Die Borduhr sollte so programmiert sein, dass sie automatisch ½T addiert, sich also auf t₀ + ½T stellt. Natürlich ist d = ½cT.
Normalerweise gucken wir auf die eigene Uhr und verlassen uns darauf, dass unsere Uhr mit einer Bezugsuhr (die in Σ als stationär beschrieben wird) synchron läuft.
Das geht im Alltag, weil wir uns im Vergleich zum Lichttempo c sehr langsam bewegen.
--- Baustelle --
Geschwindigleit und TempoLicht bewegt sich mit Lichtgeschwindigkeit
Ja, wobei es eigentlich "Lichttempo" heißen müsste. Geschwindigkeit (engl. velocity) im engeren physikalischen Sinne ist eine Vektorgröße, eine Größe mit Richtung.
Zwei Fahrzeuge, die sich beide mit 180 km/h in unterschiedliche Richtungen bewegen, haben nur dasselbe Tempo (engl. speed) – relativ zur Erde. Zwei Körper, die dieselbe Geschwindigkeit haben, bewegen sich relativ zueinander gar nicht.
Das Lichttempo wird mit c bezeichnet und ist das absolute Tempo, d.h., es ist unabhängig von der Wahl des Bezugssystems, also davon, in welchem Koordinatensystem wir rechnen und physikalische Größen beschreiben.
Eigenzeit und KoordinatenzeitFür bewegte Objekte vergeht deren Zeit langsamer
Das ist so formuliert falsch. Kein Beobachter sieht seine eigene Uhr langsamer laufen.
Der Zeittakt einer Uhr Ώ, die sich relativ zu einem Bezugskörper B mit einem Tempo v = βc bewegt, wird im von B aus definierten Koordinatensystem Σ als um den berühmten LORENTZ- Faktor
(1.1) γ = 1/√{1 − β²} = Δt⁄Δτ
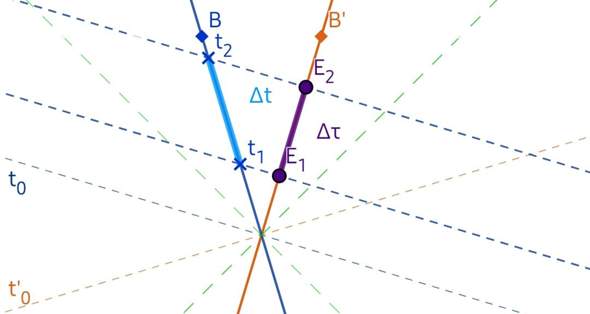
verlängert interpretiert. Dabei ist Δτ = τ₁ − τ₂ die von Ώ direkt gemessene Zeitspanne zwischen zwei Ereignissen €₁ und €₂ entlang der Weltlinie (WL) von Ώ, die Eigenzeit und Δt = t₁ − t₂ ist die von B aus ermittelte Zeitspanne zwischen diesen Ereignissen, die Σ- Koordinatenzeit.
Wie der Name sagt, ist dies eine Koordinatendifferenz in Σ, denn hierbei handelt es sich um ein raumzeitliches Koordinatensystem, dessen Zeitachse die WL von B ist.
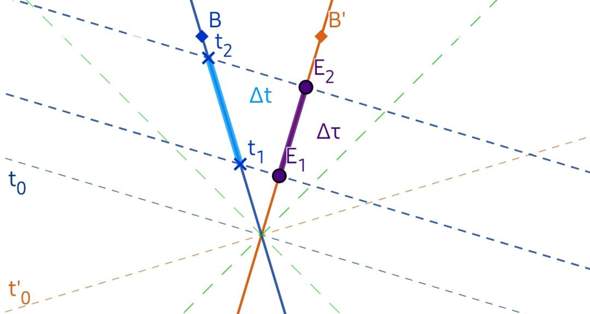
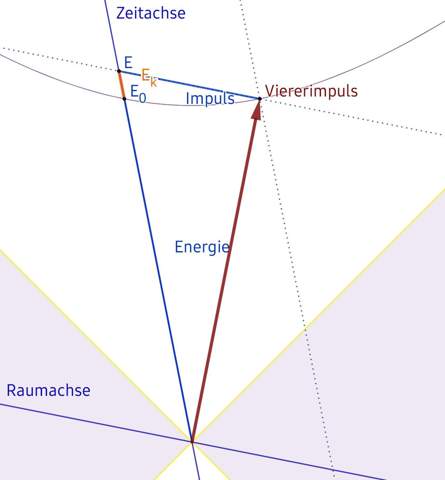
Abb. 1: Die "Zeitdilatation" ist eigentlich ein Projektionseffekt. Nicht ein durch €₁ und €₂ eingegrenzter Vorgang selbst ist in die Länge gezogen, sondern seine Projejtion auf die WL von B ist länger. In diesem Fall befindet sich Ώ in einem Körper B'.
Die Energie eines KörpersDie Masse m₀ eines Körpers ist physikalisch nichts anderes als "kondensierte" Energie, seine Ruheenergie E₀ = m₀c². In einem Koordinatensystem, in dem er sich bewegt, kommt noch kinetische Energie Eₖ hinzu. Daraus ergibt sich die Gesamtenergie
(1.2) E = (E₀ + Eₖ) = γ∙E₀.
Da Licht sich mit Lichtgeschwindigkeit bewegt vergeht für Licht keine Zeit
Das ist richtig, denn die Beziehung zwischen Δτ und den Koordinaten ist durch MINKOWSKIs Abstandsquadrat
(2) Δτ² = Δt² − Δs²⁄c²
gegeben (woraus sich auch γ herleitet), wobei Δs die in Δt zurückgelegte Entfernung ist. Bei Δs = cΔt wäre das 0.
Weil für Licht keine Zeit vergeht kann es sich auch nicht bewegen, da Geschwindigkeit Strecke/Zeit. Da keine Zeit vergeht und in dem Fall immer Null wäre bewegt es sich nicht?
Es ist genau umgekehrt: Es bewegt sich "nach eigener Uhr" (wenn es denn so etwas gäbe) unendlich schnell, da in der Gleichung für die proper velocity ("Eigen-Geschwindigkeit" = spezifischer Impuls)
(3) γv = γβc = Δs⁄Δτ
die Zeit ja im Nenner steht. Allerdings bewegst Du Dich (bzw. Dein "Jetzt") mit γ in die Zukunft, und stets ist Δs < cΔτ, wie man an (2) ablesen kann.
Bewegst Du Dich mit fast c, so bewegst Du Dich praktisch unendlich schnell durch den Raum (Entfernung d in Nullkommanix), wirst aber zugleich in Nullkommanix um d⁄c
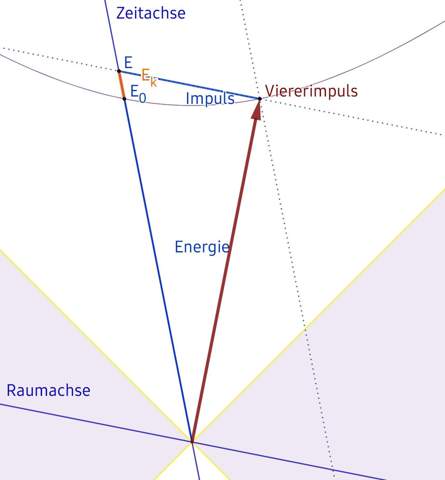
Abb. 2: Der Viererimpuls und seine Komponenten; die Vierergeschwindigkeit setzt sich entprechend zusammen
--- Baustelle ---
RaumzeitNun gibt es keine Zeitmaschinen in dem Sinne, d.h. Zeit wird nicht einfach gedehnt. Auch im Zusammenhang mit der sog. Speziellen Relativitätstheorie (SRT) ist das Wort „Zeitdilatation“ irreführend. Diese übrigens beruht komplett auf Galileis Relativitätsprinzip (RP), das besagt, dass man bei einem Bezugsobjekt O und einem anderen, relativ zu O mit einer Geschwindigkeit v› bewegten Objekt O’ ebensogut - ohne dass dies an Naturgesetzen etwas ändert - O’ als Bezugsobjekt und O als mit –v› bewegt ansehen können.
Fassen wir Raum und Zeit zur Raumzeit zusammen (was wir immer machen können und seit der SRT müssen, um gescheit zu rechnen), haben relativ zueinander bewegte Objekte O und O’ gewissermaßen unterschiedliche zeitliche Vorwärtsrichtungen.
Wer sich relativ zu O mit v› durch den Raum bewegt, der bewegt sich längs der von O aus gemessenen Zeit t automatisch auch mit dem Lorentz-Faktor
(1) γ = 1/√{1 – |v›|²/c²} > 1
und mit γ·v› - nach eigener Uhr - durch den Raum. Seine Geschwindigkeit ist der Quotient
(2) (Δs›/Δτ)/(Δt/Δτ) = Δs›/Δt,
und dessen Betrag bleibt immer unter c. Wenn man so will, käme sich Licht unendlich schnell vor.
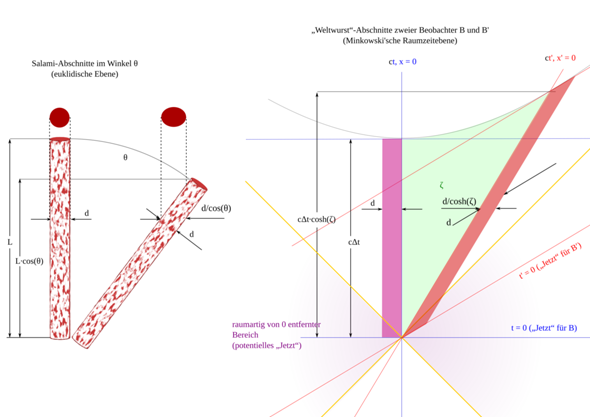
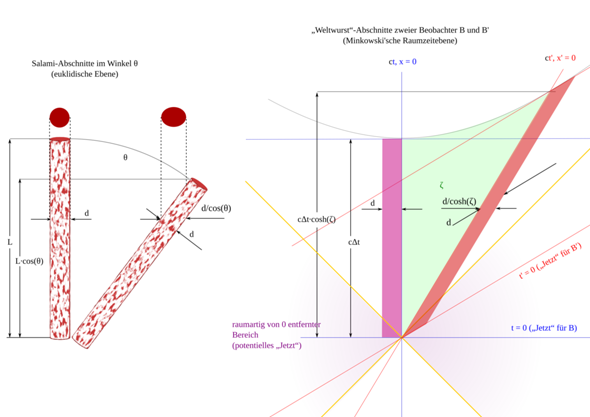
Zur Abstandsdefinition in der Raumzeit habe ich ein Bild erstellt:

Vor diesem Hintergrund ist auch die „Längenkontraktion“ keine Kontraktion, sondern ein „Schrägschnitt durch die Weltwurst“.
Die Relativitätstheorie sollte eigentlich einfach Klassische Physik heißen.
Das, was wir unter diesem Namen kennen, sollte künftig Klassische Physik genannt werden, weil sie eine Näherung für spezifische potentielle bzw. kinetische Energien ist, deren Beträge klein im Vergleich zu c² sind und der Unterschied zwischen τ und t bzw. t’ vernachlässigt werden kann.
Das sind die tatsächlichen Verhältnisse, nicht etwa so, wie es aus historischen Gründen immer noch gelehrt wird: Der Newton-Limes als die (normale) Klassische Physik und unter ,ferner liefen’, für die ganz Abgedrehten bzw für ganz abgefahrene Spezialfälle eine Extra-Theorie. Nein, ,Newton’ ist der Spezialfall, ,Einstein ‘05’ (SRT) ein allgemeinerer und ,Einstein ‘15’ (ART) ein noch allgemeinerer Fall.
_____________________
¹) Das Beispiel mit v=0,6c ist besonders einfach zu rechnen, weil 3, 4 und 5 ein Primitives Pythagoreisches Tripel ergeben, d.h. 3² + 4² = 5², und so ist 1 − 0,6² = 0,8².
___
s. auch diesen Kommentar.

Deine Überlegung stimmt.
Aber du hast eine andere, ebenso wichtige, Eigenschaft der Relativitätstheorie übersehen: nicht nur verlängert sich die Zeit, es verkürzt sich auch der Raum.
Da das Licht sich mit Lichtgeschwindigkeit uns gegenüber bewegt, vergeht für das Licht keine Zeit, aber die Strecke, die wir wahrnehmen, schrumpft für das Licht auf 0 zusammen. Das Licht braucht sich also auch (von ihm selbst aus gesehen) überhaupt nicht zu bewegen, weil Quelle und Ziel zusammenfallen.
…aber die Strecke, die wir wahrnehmen, schrumpft für das Licht auf 0 zusammen.
Das ist unglücklich formuliert. Da schrupft ja nichts, sondern wenn man ernsthaft - mit mathematischen Tricks wie der Nichtstandardanalysis, um nicht durch 0, sondern nur durch etwas Infinitesimales teilen zu müssen - eine Art „Ruhesystem des Lichtsignals“ konstruiert, ist in diesem die Strecke infinitesimal.
Übrigens ist dann auch die Wellenlänge des Lichts unendlich groß.
Das ist sie übrigens ohnehin, denn die eigentliche Länge einer Strecke ist ja
Δς := √{Δs² – c²Δt²},
und im oben genannten Fall ist
cΔt ≈ Δs => Δς ≈ 0.
Für einen im Zug Mit"fahrenden" würde der Zug nur für einen unendlich kurzen Moment beschleunigen und wieder abbremsen, aber für seine Bewegung keine Zeit brauchen (Relativität der Bewegung).
Allerdings kann es einen solchen Beobachter nicht geben, da kein materieller Gegenstand tatsächlich auf Lichtgeschwindigkeit beschleunigt werden kann, er bleibt immer langsamer, wenn auch möglicherweise nur sehr, sehr wenig. (Immerhin würde ein solcher Beobachter eine sehr starke Beschleunigung und ein sehr starkes Abbremsen innerhalb einer sehr kurzen Zeit beobachten und später davon berichten können. Natürlcih nur, falls er robust genug für diese Beschleunigungen ist.)
Es gibt drei Bereiche, zwischen denen es nach der Speziellen Relativitätstheorie keine Übergänge gibt, die also streng voneinander getrennt sind:
- raumartige, das ist der Bereich, in dem wir uns bewegen und der unsere Alltagserfahrung ausmacht -- was sich hier befindet, hat immer eine Geschwindigkeit unterhalb der Lichtgeschwindigkeit
- lichtartige, das ist der Bereich, in dem sich das Licht bewegt und ebenso alles andere, das sich mit Lichtgeschwindigkeit bewegt -- was sich hier befindet, hat immer genau Lichtgeschwindigkeit ("langsameres" Licht durch Brechungsindizes sind ein anderes Phänomen)
- zeitartige, das ist der Bereich, der nach allem was wir wissen nur Strukturen zugänglich ist ("Tachyonen" sind bisher rein hypothetisch) -- was sich hier befindet, hat immer eine Geschwindigkeit oberhalb der Lichtgeschwindigket (Beispiele: Lichtfleck eines Lasers, der den Mond anstrahlt und dabei gedreht wird; elektromagnetische Wellen in einem Hohlleiter)
Da das Licht sich mit Lichtgeschwindigkeit uns gegenüber bewegt, vergeht für das Licht keine Zeit...
...wobei sich in dieser Nullzeit alles abspielt und das Licht jede beliebige Strecke zurücklegt. Es käme sich also - wenn es etwas wahrnehmen könnte - unendlich schnell vor, nicht stehend.
...aber die Strecke, die wir wahrnehmen, schrumpft für das Licht auf 0 zusammen.
Wenn es sich selbst ohnehin als ruhend betrachten würde, was es könnte, aber nicht müsste.
Wir hätten hier einen Ausdruck der Form 0/0. Also einen nicht definierten Ausdruck. Überhaupt beruht alles, was wir über ein Bezugssystem sagen können, das sich mit Lichtgeschwindigkeit bewegt, auf Ausdrücken dieser Form.
Wir können also allenfalls etwas über sehr schnell bewegte Systeme sagen und schauen, ob beim Grenzübergang u_rel -> c etwas vernünftiges herauskommt.
Falls das Photon eine Ruhmasse hat (einige Physiker denken dies), könnten wir tatsächlich etwas darüber aussagen, wie das Licht seine Reise wahrnimmt.
(Dabei fällt mir eine andere Frage ein -- könnten wir dann auch rein hypothetisch überhaupt noch mit Tachyonen wechselwirken?)
Wir hätten hier einen Ausdruck der Form 0/0. Also einen nicht definierten Ausdruck. Überhaupt beruht alles, was wir über ein Bezugssystem sagen können, das sich mit Lichtgeschwindigkeit bewegt, auf Ausdrücken dieser Form.
Natürlich. Das von mir oben Geschriebene ist auch quasi ins Unreine geschrieben und darf auf keinen Fall zu ernst genommen werden. Das habe ich aber auch oben schon geschrieben.
Wir können also allenfalls etwas über sehr schnell bewegte Systeme sagen und schauen, ob beim Grenzübergang u_rel -> c etwas vernünftiges herauskommt.
Oder wir wenden den Trick mit der Nichtstandard-Analysis an und schreiben dem Photon eine infinitesimale Masse zu. Mathematisch wären wir damit auch „sauber“.
Falls das Photon eine Ruhmasse hat (einige Physiker denken dies),...
Könnte was dran sein, allein schon, weil das Universum vielleicht eine endliche Ausdehnung hat. In einem Experiment konnte man Photonen eine Quasi-Masse geben, indem man sie zwischen zwei Spiegeln eingesperrt hat, wodurch sie eine Mindestenergie hatten - technisch also eine „Masse“. So konnte man sie sogar Bose-Einstein-kondensieren lassen.
Dabei fällt mir eine andere Frage ein -- könnten wir dann auch rein hypothetisch überhaupt noch mit Tachyonen wechselwirken?
Wenn es eine solche Wechselwirkung geben sollte, müsste sie streng zeitsymmetrisch sein, nicht nur von der Möglichkeit her, sondern auch faktisch. Beispielsweise müsste eine eventuelle Absorption ebenso stark erfolgen wie die Emission. Schließlich haben raumartig getrennte Ereignisse keine feste zeitliche Reihenfolge.
Nebenbei ist dieser Umstand für uns als Beobachter auch nicht von Belang. Für uns vergeht Zeit also kann sich das Licht von außen betrachtet problemlos bewegen.
Die Zeit in einem Zug der mit Lichtgeschwindigkeit fährt würde hypothetisch von außen betrachtet auch stillstehen, der Zug selbst würde sich aber dennoch bewegen.