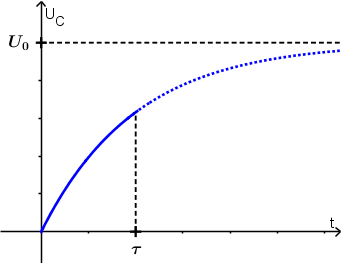
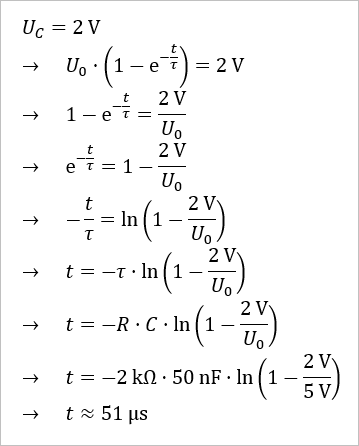Zeit von Uc?
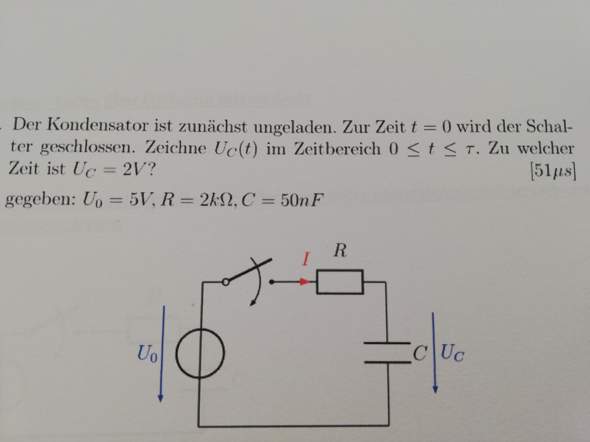
Weiß jemand eine nützliche Formel für diese Aufgabe? Bzw Rechenweg
3 Antworten
Das ist die Standardschaltung zum Aufladen eines Kondensators.
Zum Zeitpunkt 0 ist der KOndensator ohne Ladung und ohne Spannung. Also fließt der maximale Strom durch den Widerstand.
Dieser Strom sammelt sich auf dem Kondensator, so dass dort auch eine Spannung (zwischen den Platten des Kondenators) entsteht. Diese Spannung wirkt der Spannung in der Spannungsquelle entgegen. Deshalb weniger Spannungsabfall über dem Widerstand und damit auch weniger Striom zum weiteren Aufladen des Kondensators.
Das ganze endet dann in der Exponentialfunktion zum Aufladen des Kondensators.
u(t) = U0 ∙ (1 - exp (- t / τ) ) ; τ = R ∙ C
Gruß, H.
Für den Ladevorgang eines Kondesators mit Kapazität C über einen ohmschen Widerstand R und mit einer Spannung von U[0] erhält man für die am Kondensator anliegende Spannung U[C](t) zum Zeitpunkt t (wobei der Kondensator bei t = 0 ungeladen sei)...

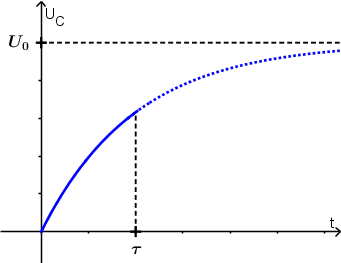
Man kann sich auch merken:
Zum Zeitpunkt t = τ ist der Kondensator zu etwa 63 % geladen.
============
Zu welcher Zeit ist nun U[C](t) = 2 V?
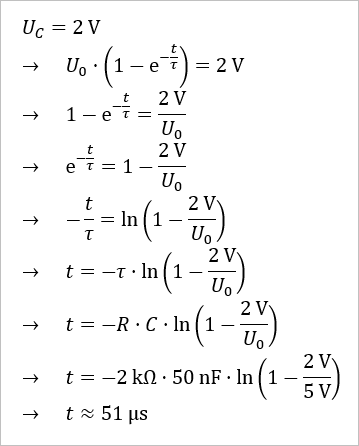
Nach etwa 51 μs ist U[C] = 2 V.