Wie viele verschiedene Ergebnisse erhalte ich nach n mal Würfeln?
- Beispiel: homogener Würfel. - für 1. Wurf: 1, für 2. Wurf: 1,83 (11/6), ...
- Beispiel: es wird jede Sekunde eine Zufallszahl zwischen 1 und 100 erstellt. Wie viele Verschiedene Zufallszahlen erhalte ich nach wie vielen Sekunden.
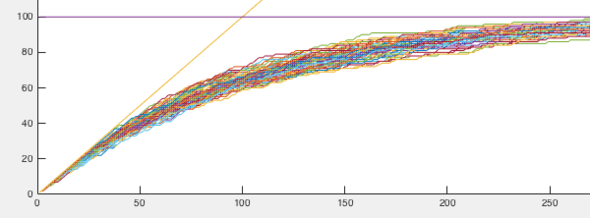
Eine Simulation von Beispiel 2 habe ich bereits durchlaufen lassen. die Kurve wird begrenzt durch die Geraden f(x) = x und g(x) = 100
3 Antworten
1.
nach Wurf n:
Chance dass du bisher nur 1 Zahl erreicht hast:
(1/6)^(n-1) = x1
Chance dass du bisher genau 2 Zahlen erreicht hast
(2/6)^(n-2) - x1 = x2 (n >= 2)
Chance dass du bisher genau 3 Zahlen erreicht hast
(3/6)^(n-3) - x2 = x3 (n>=3)
usw.
2. Entsprechend nur mit 100 statt 6.
Hoffe das hilft ;)
das ergibt sich ja aus dem was du geschrieben hast. wenn ich x2 abziehe und einsetze muss ich x1 auch abziehen.. oder meinst du doppelt?
(3/6)^(n-3) - x1 -x2 = x3 (n>=3)
Die Zeile muss so aussehen, also beide abziehen, nicht doppelt.
x2 = ... - x1 würde dann aber bedeuten, dass ich es doppelt abziehe. Verstehst du was ich mit doppelt meine?
X1 = Wahrscheinlichkeit, bisher genau 1 Zahl erwischt zu haben.
X2 = Wahrscheinlichkeit, bisher genau 2 verschiedene Zahlen erwischt zu haben.
X1 ist nicht in X2 enthalten, daher musst du beide abziehen und wenn du das tust, ziehst du keines doppelt ab. In der Zeile vorher haben wir ja x1 aus dem Term rausgenommen.
(3/6)^(n-3) - ((2)/6)^(n-2) = x3 ginge auch, wahrscheinlich sogar besser zu benutzen.
Allgemein xy = (y/6)^(n-y) - ((y-1)/6)^(n-y-1)
Kein schlechter Ansatz. Ich versuche das mal in eine Form zu bringen, die mir weiter hilft. Kommst du auch auf die Möglichkeiten anstatt Wahrscheinlichkeiten?
Die Frage nach den Möglichkeiten ist mir nicht ganz klar, du hast ab n>= 6 doch offensichtlich nur 6 mögliche Zustände in dem dein System sein kann.
Schau dir am besten die Grafik an. Diese Kurven zeigen auf, wie viele unterschiedliche Ergebnisse gefunden wurden abhängig von den Versuchen(x). Die Zustände kann ich erst sagen wenn ich in einem späteren Zeitpunkt bin. Ich möchte den mittlere Graphen stochastisch bestimmen.
Programmiere die obere Formel, dann lass für jedes n den Wert mit der höchsten Wahrscheinlichkeit bestimmen max(x1;x2 ...;x100) und plote diesen Wert, dann hast du den Graphen, den du suchst.
Der Ansatz von AnglerAut ist schon gar nicht so schlecht, muß aber noch ein bißchen aufgearbeitet werden.
Wenn Du einen 6-seitigen Würfel hast dann ist die Wahrscheinlichkeit, daß Du in N Würfen immer nur die 1 siehst:
(1/6)^N
Für jede andere Zahl gilt natürlich die gleiche Wahrscheinlichkeit.
Die Wahrscheinlichkeit, daß Du in N Würfen nur die 1 siehst ODER nur die 2 siehst ODER nur die 3 siehst ODER nur die 4 siehst ODER nur die 5 siehst ODER nur die 6 siehst ist
(1/6)^N + (1/6)^N + (1/6)^N + (1/6)^N + (1/6)^N + (1/6)^N
Das ist also, wie AnglerAut schon gesagt, hat die Wahrscheinlichkeit dafür, daß Du nach N Würfen nur eine einzige Zahl gesehen hast.
Die Wahrscheinlichkeit dafür, daß Du nach N Würfen in den ersten k die 1 und in den letzen N-k die zwei siehst ist
(1/6)^k * (1/6)^(N-k) = (1/6)^N
Jetzt könntest Du aber auch im ersten Wurf die 2 sehen, dann k mal die 1, dann N-k-1 mal, die 2. Oder Du könntest 2 und 1 in irgendeiner anderen Kombination sehen, wobei die 1 insgesamt k mal und die 2 insgesamt N-k mal auftaucht. Die Anzahl an Kombinationsmöglichkeiten ist
N! / ( k! * (N-k)! )
Also ist die Wahrscheinlichkeit nach N Würfen 1 uns 2 in irgendeiner Kombination zu sehen wobei die 1 k mal und die 2 N-k mal auftaucht
N! / ( k! * (N-k)! ) * (1/6)^(N)
Natürlich könnte die 1 auch nur k-1 mal und die 2 N-k+1 mal auftauchen oder die 1 k+1 mal und die 2 N-k-1 mal auftauchen. Insgesamt kann die 1 einmal bis N-1 mal auftauchen (und die 2 dann entsprechend viele male so daß Du N Würfe hast). Die Wahrscheinlichkeit, daß die 1 einmal auftaucht und die 2 N-1 mal ODER daß die 1 zweimal auftaucht und die 2 N-2 mal ODER ... ODER daß die 1 N-1 mal auftaucht und die 2 einmal ist
Summe von k=1 bis N-1 N! / ( k! * (N-k)! ) * (1/6)^(N)
Du hättest auch ein anderes Zahlenpaar wählen können, 1 und 4 zum Beispiel oder 5 und 6. Insgesamt gibt es 6*5 = 30 mögliche Zahlenpaare. Die Wahrscheinlichkeit, daß Du in N Würfeln genau ein Zahlenpaar siehst, also nur zwei Zahlen beobachtest ist
30 * Summe von k=1 bis N-1 N! / ( k! * (N-k)! ) * (1/6)^(N)
Hier stimmt AnglerAuts Formel jetzt nicht mehr. Laß uns zur Probe N=4 wählen. Nach AnglerAut hast Du
(2/6)^(4-2) - (1/6)^(4-1) = (2/6)^2 - (1/6)^3 = 23/216
Nach unserer Formel erhältst Du
30 * Summe von k=1 bis 3 4! / ( k! * (4-k)! ) * (1/6)^(4) =
30 * (1/6)^(4) * Summe von k=1 bis 3 4! / ( k! * (4-k)! )
30 * (1/6)^(4) * ( 4 + 6 + 4 ) = 420/1296 = 70/216
Laß uns jetzt die Wahrscheinlichkeit berechnen, daß Du in N Würfen genau 3 Zahlen siehst. Die Argumentation läuft so ähnlich wie für zwei Zahlen. Wir können wieder damit anfangen, daß drei bestimmte Zahlen mit einer ganz bestimmten Häufigkeit und in einer ganz bestimmten Reihenfolge auftauchen. Dann können wir wieder unterschiedliche Reihenfolgen betrachten und dannunterschiedliche Häufigkeiten berücksichtigen. Zum Schluß überlegen wir uns dann noch wie viel Möglichkeiten es gibt drei Zahlen zu wählen. Das sind 6*5*4 = 120 Möglichkeiten. Die Wahrscheinlichkeit genau drei Zahlen in N Würfen zu sehen ist
120 * Summe von k=1 bis N-2 Summe von h=1 bis N-k-1 N! / ( k! * h! * (N-k-h)! ) * (1/6)^(N)
Hier ist k, die Häufigkeit mit der die erste Zahl auftaucht und h, die Häfigkeit mit der die zweite Zahl autaucht.
Unser Ergebnis können wir jetzt verallgemeinern wenn Du für einen sechseitigen Würfel die Wahrscheinlichkeit ausrechnen möchtest, daß Du in N Würfen genau m Zahlen siehst, dann bestimmst Du zunächst wie viele Möglichkeiten es gibt m Zahlen von 6 zu wählen. Das sind 6!/m! Möglichkeiten. Dieser Wert schreibst Du dann als Faktor vor die Summen (dort wo die 120 in der obigen Formel steht). Bei m Zahlen mußt Du die Formel über m-1 Summen laufen lassen. Die erste Summe läuft von k=1 bis k=N-m+1, die zweite Summe läuft von h=1 bis h=N-k-m+2, die dritte Summe läuft von j=1 bis j= N-k-h-m+3 und so weiter...
Für einen hundertseitigen Würfel sieht es ganz ähnlich aus. Du ersetzt einfach das 1/6 gegen 1/100. Und aus 6!/m! wird jetzt 100!/m!
Solche Formeln sind natürlich ein bißchen kompliziert um sie auf einem Blatt Papier auzurechnen, aber wenn Du programmieren kannst, kannst Du eine Funktion schreiben, die Dir das Ergebnis liefert.
Es ist halb drei. Da wird kein Mathe mehr gemacht.
1+1=2. Mehr macht das Hirn um die Uhrzeit nicht mit.
kleine Korrektur:
Du musst für xn alle x1 bis x(n-1) abziehen.