Wie viele Konformationsisomere entstehen bei Butan?
also ich würde sagen vier, denn dort wo die Energie gleich ist, so ist das eine Konformation… wie würdet ihr das besser formulieren?
4 Antworten
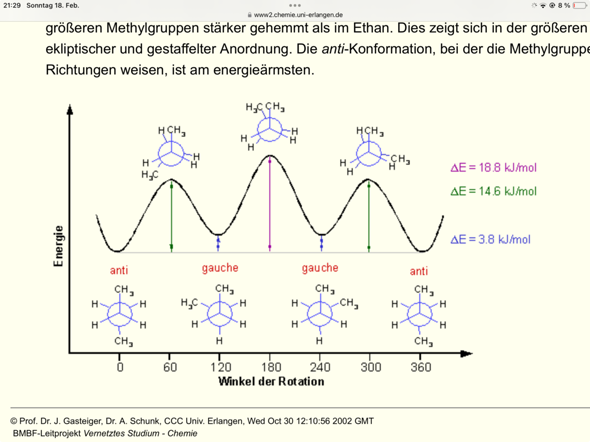
Bei Winkeln gilt 0° = 360°. Also gibt es nur drei Konformformere, nämlich die antiperiplanare (0°) und die beiden synclinalen (±120 °).
Nur die Minima auf der Potentialkurve sind Konformere, die Maxima nicht.
Aber 60 Grad und 300 grad doch auch, wenn ich das Molekül wie bei einem Blatt einmal umdrehen würde
Du siehst doch, daß bei ±60° (und bei 180°) die Maxima der Potentialkurve liegen — das ist auch so zu erwarten, weil die Atome dabei genau hintereinander stehen (Diederwinkel Null). Daher sind diese Strukturen nicht stabil, sondern wandeln sich sofort in etwas anderes um.
Die Minima bei 0°C und ±120° sind dagegen grundsätzlich stabil — bei Raumtemperatur können sie sich zwar ineinander umwandeln, aber man kann sie ja abkühlen und dann sind sie in ihrem Minimum gefangen.
Es gibt dementsprechend nur gestaffelt und verdeckte Konformationsisomere. Dies werden nicht nochmal unterteilt, je nach dem welche Grupppe (bspw. Methylgruppe und H-Atom oder H-Atom und H-Atom) z.B oben verdeckt ist?
Die verdeckten (±60°, 180°) sind sind keine Konformere, weil sie Maxima in der Potentialkurve sind und daher nicht stabil. Das Konformer bei 0° heißt antiperiplanar (oder transoid oder sonstwie), die beiden bei ±120° heißen synclinal (oder cisoid oder gauche oder was auch immer; sie verhalten sich wie Bild und Spiegelbild). Diese Unterscheidung geht aber natürlicjh nur, wenn das Substitutionsmuster es zuläßt; im C(CH₃)₃–CH₃ gibt es z.B. drei gleichwertige Minima, also nur ein Konformer.
Es tut mir so unfassbar leid, dass ich so schwer von Begriff bin, aber mein Lehrer sieht auch diese als Konformer im in entferntesten Sinn an.
drei gleichwertige Minima, also nur ein Konformer.
Aber dies ist doch gar nicht der Fall! Schauen Sie sich doch mal das Bild an.
im C(CH₃)₃–CH₃ gibt es z.B. drei gleichwertige Minima, also nur ein Konformer.
Das ist ja nicht der Vogel, auf den sich Deine Potentialkurve bezieht (ich hätte auch CCl₃–CH₃ oder sogar CH₃–CH₃ als Beispiele wählen können).
unten: Nr.1 = Nr4
Hi,
Konformere gibt es viele.
Die energetisch günstigsten liegen allerdings bei den Tiefpunkten. Das sind die anti- und die gauche-Konformationen. Die Anti-Konformationen entsprechen allerdings einander, da 0° = 360°, also eine ganze Umdrehung entlang der C2-C3-Einfachbindung.
Also: Es gibt prinzipiell viele Konformere, hier sind sechs Stück abgebildet - nur drei davon sind aber energetisch günstig (nämlich bei 0° = 360°, 120° und 240°).
LG
Aber wenn ich lediglich eine Drehung von 60 grad beachte? dann vier?
Ich schrieb: Es gibt prinzipiell sieben Konformere (0° = 360°, 60°, 120°, 180°, 240°, 300°). Aber nur diejenigen bei 0° = 360°, 120° und 240° sind die energetisch bevorzugten Konformere (in den "Tälern" des Graphen).
Sind aber 60 Grad und 300 grad nicht das Molekül, weil ich diese wie bei einem Blatt einmal umdrehen kann und diese dann deckungsgleich sind?
Es gibt doch unendlich viele...deshalb ist da eine durchgezogene Linie!
Aber es gibt natl. zwei Hauptkonformere...Anti und gauche! Wobei sich zein gauche Konformere wie Bild und Spiegelbild verhalten.
aber was ich wenn ich lediglich eine drehung von 60 grad beachte? dann habe ich lediglich 4
aber auch die syn Positionen sind möglich, wenn auch nicht wahrscheinlich!
aber ich habe: 0 grad, bei 60 und 300 dieselben, bei 120 und 240 isomere und bei 180 dann welche!