Wie viele dreistellige Zahlen kann man mit 6 Ziffern bilden?
Wieviele dreistellige Zahlen kann man mit den Ziffern 2, 3, 5, 6 ,7 und 9 bilden? Und wie finde ich heraus wieviele davon kleiner sind als 400? (Ohne zurücklegen)
2 Antworten
Das ist eine schöne Kombinatorik-Aufgabe.
Da kennst du sicherlich schon ein paar Formeln dazu...
Wir müssen uns noch überlegen, wieviele mögliche Ziffern wir zur Auswahl haben, wie viele davon wir jeweils auswählen (Erinnerung: dreistellige Zahl...) und ob wir hier den Fall mit oder ohne Zurücklegen haben. (anders formuliert: darf dieselbe Zahl mehrfach vorkommen oder nicht)
Mit diesen Überlegungen kannst du die richtige Formel auswählen, die passenden Zahlen einsetzen und den ersten Teil deiner Frage beantworten.
-------------------------------------------------------------------------------------------------------------------------------------
Ergänzung:

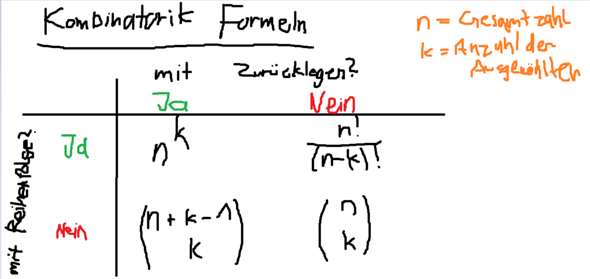
Hier ein Schema, um die richtige Formel auszuwählen. Einfach die beiden Fragen am Rand beantworten und das richtige Feld auswählen :)
---------------------------------------------------------------------------------------------------------------------------------
Ergänzung:
Wir wählen also: ohne Zurücklegen, aber mit Reihenfolge (123 ist ja nicht dasselbe wie 321).
Also verwenden wir die Formel
wobei n = 6 und k = 3.
Was hier inhaltlich passiert ist Folgendes.
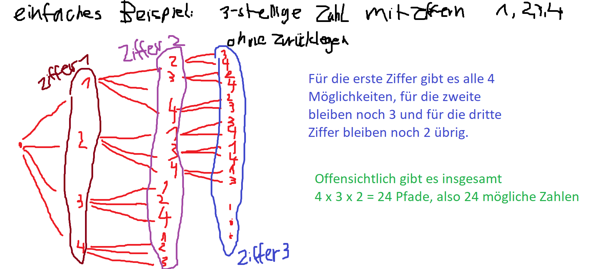
Die erste Ziffer unserer dreistelligen Zahl darf eine von sechs möglichen sein.
Für die zweite Ziffer bleiben noch fünf mögliche Ziffern und für die dritte noch drei mögliche Ziffern. Die möglichen Zahlen ergeben sich dann durch die Multiplikation dieser Zahlen (das kann man sich mit einem Wahrscheinlichkeitsbaum ganz gut klar machen, siehe Bild):

Jetzt sollen die Zahl aber kleiner sein als 400. Dreistellige Zahlen sind genau dann kleiner als 400 wenn die erste Ziffer höchstens eine 3 ist....
Überlege dir mal, welche Stelle dann durch wieviele mögliche Zahlen besetzt werden kann und multipliziere diese.
Sehr gut! Das ist absolut korrekt :)
Nein, das lässt sich nur schwer formalisieren... Deshalb ist es wichtig, dass man versteht, welche Überlegungen hinter den Formeln stecken, dann sieht man ja auch, was man für solche Spezialfälle ändern muss. Und das hat ja schon ganz gut geklappt, oder? :)
Stimmt, wir können die Aufgabe in zwei Teile teilen:
- für die erste Ziffer haben wir zwei mögliche Zahlen und eine wird gezogen, also 2!/(2-1)! = 2/1 = 2
- für die beiden anderen Ziffern haben wir fünf Möglichkeiten und zwei werden gezogen, also 5!/(5-2)! = 5!/3!
Setzt man diese beiden Formeln hintereinander, erhält man @Aurel8317648 's Lösung.
Hab jetzt den ersten Teil der Frage beantwortet, das Ergebnis lautet 120. Verstehe aber jetzt noch nicht ganz mit welcher Formel/Methode ich darauf komme, wie viele Zahlen unter 400 sind.
Hey ich schaue mir das jetzt seit 40 Minuten an, wie zur Hölle errechnet man alle Zahlen unter 300 wenn du die Ziffern 1,2,3,4,5,6,7,8,9 hast? Das ergeben 648 Möglichkeiten, aber ich verstehe nicht wie du hier auf die 6!/3! kommst, die 6 - wahrscheinlich weil es 6 Ziffern gibt - bei mir sind es 9 - aber was hat es mit der 3 auf sich? Denn 9!/3! wären über 60.000 und das ist unmöglich - bitte helfen - dieser Thread ist leider der einzige im deutschsprachigen Internet über das Thema größer/kleiner aus konstruierten Zahlen.
Ich habe ja oben dieses Formelschema aufgemalt. Die 6!/3! kommt so zustande: Wir dürfen jede Ziffer nur einmal verwenden, also sind wir in der Spalte "ohne Zurücklegen". Bei Zahlen spielt die Reihenfolge natürlich eine Rolle (12 ist ja nicht die gleiche Zahl wie 21), wir sind also in der Zeile "mit Reihenfolge". Die Formel ist also n!/(n-k)!. n ist dabei die Anzahl der Dinge, die man zur Verfügung hat. Bei dir sind das die Ziffern, also n = 9. k ist die Anzahl der Dinge, die man auswählt, wir wählen drei Ziffern aus, da wir ja dreistellige Zahlen basteln, also k = 3.
Oben galt ja n = 6, und k = 3, also n!/(n-k)! = 6!/(6-3)! = 6!/3! = 120.
Bei dir (im Allgemeinen Fall) gilt: n = 9, und k = 3, also n!/(n-k)! = 9!/(9-3)! = 9!/6! = 504
Jetzt gibt es aber noch eine Einschränkung: Wir suchen nur die Zahlen, die kleiner sind als 300. Da das ein spezieller Fall ist, gibt es dafür keine allgemeine Formel.
Wir erinnern und an ein Grundprinzip der Wahrscheinlichkeitsrechnung: Wenn mehrere Dinge gleichzeitig gelten, rechnet man "mal".
Schauen wir uns jetzt alle Ziffern einzeln an und überlegen, wieviele Möglichkeiten es für jede Ziffer gibt. Dreistellige Zahlen, die kleiner sind als 300, fangen mit 1 oder 2 an, für diese Stelle gibt es also nur 2 Möglichkeiten. Für die zweite Stelle können wir eine beliebige Ziffer nehmen, allerdings nicht die von der ersten Stelle, es gibt also noch 9-1=8 Möglichkeiten. Für die dritte Stelle ist ebenfalls die einzige Vorgabe, dass es nicht die Ziffer von der ersten oder zweiten Stelle sein darf, zwei Ziffern fallen also weg. Es gibt also noch 9-2=7 Möglichkeiten für die dritte Stelle.
Es gibt also zwei Möglichkeiten für die erste Stelle UND acht Möglichkeiten für die zweite Stelle UND sieben Möglichkeiten für die dritte Stelle. Also insgesamt 2*8*7 = 112 mögliche Zahlen.
Mit den richtigen Hilfestellungen auf jeden Fall! Und darauf wollen wir doch hinarbeiten, oder? :)
Edit: Standen da nicht eben noch 7 Ziffern?
Edit2: Ach und plötzlich auch ohne zurücklegen? :)
ja , da stand was anderes
6*5*4/3*2*1 = 20 soll die richtige Lösung sein , aber ohne wiederholung , was der FS nicht angemerkt hat ( so wie 333 )
Ok, war kurz irritiert, ob ich nicht mehr bis 7 zählen kann.
Nicht ganz. So aufgeschrieben sollte es 6*5*4*3*2*1/(3*2*1) = 6*5*4 = 120 heißen.
Das dachte ich mir, es gilt aber 6!/3! = 6*5*4*3*2*1/(3*2*1) = 6*5*4 = 120 :)
Danke, ja bin dann durch einen anderen Antworter draufgekommen dass ich in meiner Eile die Angabe ein bisschen falsch geschrieben hatte - Entschuldigung für die Verwirrung!
Danke, verstehe es jetzt. Die zweite Aufgabe löse ich also einfach mit 2*5*4 - lässt sich das auch irgendwie allgemeiner in einer Formel mit n und k ausdrücken? Nicht wirklich oder?