Wie stellt man kinematische zwangsbedingung auf?
Hey leute, wir sollen in b) die Kinematische zwangsbedingung aufstellen. Ich habe mir die Lösung angeguckt und kann die absolut nicht nachvollziehen weil ich echt nicht weiß wie das zustande gekommen ist. Bin seit stunden am überlegen und recharchieren finde jedoch nichts darüber.
Ich hoffe ihr könnt mir erklären was genau damit gemeint ist und wie man das aufstellt.
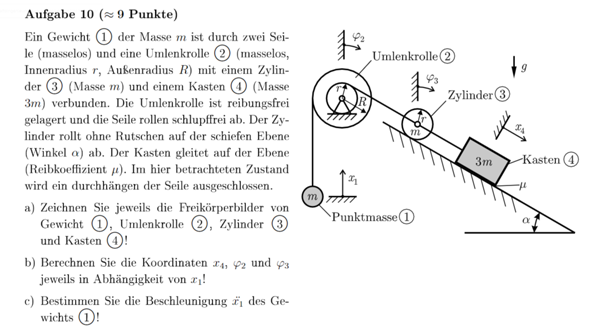
2 Antworten
Wenn du am Kasten (4) ziehst, drehen sich die Rolle (2) und das Zylinder (3) und die Masse (1) wird angehoben. Für jede Position des Kastens sind die Positionen der anderen drei Objekte eindeutig festgelegt. Das ist die kinematische Zwangsbedingung, eine Bedingung, die uns sagt, welche Werte die drei Koordinaten in Abhängigkeit von der vierten annehmen.
Wie wäre es, wenn du erst mal nur Kasten und Masse anschaust. Sagen wir, r und R wären gleich, wie würden dann x1 und x4 zusammenhängen?
Was du geschrieben hast, ist kein Zusammenhang sondern ein Term, wo x1 und x4 auftauchen. Ein Zusammenhang sollte immer ein Gleichheitszeichen beinhalten, wie bei einer Funktionsdefinition.
Meine andere antwort wäre dann x1*r=x4*r, aber sonst wüsste ich echt nicht weiter leider
Das sieht schon viel besser aus. ;) Nun kannst du ja in dem Fall beide Seiten der Gleichung durch r teilen und hast dastehen x1=x4. Also, wenn ich den Kasten um 2m schiebe, hebt sich das Gewicht auch um 2m.
Wie ist es denn, wenn nun r und R nun doch nicht gleich sind?
wäre das dann: x1*R=x4*r dann umstellen evt nach x4: x4=x1*R/r ?
Nicht ganz. ;)
Vielleicht wird es doch klarer, wenn wir erst mal eine Verbindung zwischen x1 und phi2 herstellen. Hast du da eine Idee?
Tipp: Wie lässt dich die Bogenlänge eines Kreisbogens mit Radius r und Öffnungswinkel alpha berechnen?
jetzt bin ich aber komplett durcheinander xd. Bogenlänge würde ich einfach mal pi*R^2*alpha/360 sagen
Das ist keine Bogenlänge sondern die Fläche eines Kreissektors. ;)
Gleichgewichtsbedingungen sind:
1) Die Summe aller Kräfte in eine Richtung ist zu jedem Zeitpunkt gleich NULL
2) Die Summe aller Drehmomente um einen Punkt ist zu jedem Zeitpunkt gleich NULL.
Vorgehensweis:
1) die Bewegungsrichtung festlegen,indem du einen Pfeil einzeichnest
2) ein x-y-Koordinatensystem einzeichnen.Kräfte in positiver y-Richtung=positiv und die Kräfte in der Richtung der Bewegungsrichtung sind positiv
3) die Trägheitskraft F=m*a wirkt immer entgegen der Bewegungsrichtung
4) an der kleinen Rolle wirkt am Umfang die Reibkraft Fr
5) hier ergeben sich 3 Gleichungen
5.1) die Masse m
5.2) die kleine Umlenkrolle
5.3) die Masse 3m
wegen m<3m bewegt sich das System der schiefen Ebene hinab.Also bewegt sich die Masse m nach oben
Kräfte an der Masse m:Die Summe aller Kräfte ist zu jedem Zeitpunkt gleich NULL
Fs1-Fg-F=0
1.te Formel Fs1=Fg+F=m*g+m*a
Fs1=Seilkraft,wirkt nach oben → positiv
F=m*a Trägheitskraft,wirkt entgegen der Bewegungsrichtung,wirkt nach unten → negativ
Fg=m*g Gewichtskraft,wirkt nach unten → negativ
Kräfte und Momente an der Zylinderrolle
Fs2-Fr-Fsr=0
2.te Formel Fs2=Fr-Fsr=Fr+Fs1*R/r Kräfte an der Zylinderrolle
Fs2=Seilkraft zwischen Zylinderrolle und der Masse m3 → positiv wirkt in Bewegungsrichtung
Fr=Reibkraft zwischen Zylinderrolle und schiefer Ebene
Fsr=Seilkraft zwischen Umlenkrolle und Zylinderrolle → negativ wirkt entgegen der Bewegungsrichtung
Mr-Mt=0
M=Mt
Fr*r=J*(phi)´´
3.te Formel Fr=J/r*(phi)´´
M=Fr*r ist das Drehmoment aus der Reibkraft Fr und dem Radius der Zylinderrolle
Mt=J*(phi)´´ ist das Trägheitsdrehmoment,was entgegen der Bewegungsrichtung wirkt
J=Massenträgheitsmoment der Zylinderrolle
(phi)´´=Winkelbeschleunigung in rad/s² (Radiant pro Sekunde zum Quadrat)
Umrechnung: a/r=(phi)´´ → a=Beschleunigung in m/s²
Kräfte an der Masse m3
Fh-Fr2-F-Fs2=0
Fh=Fr2+F+Fs2=m*a+Fs2 mit Fh=Fg*sin(a)=(m3)*g*sin(a)
Fr2=Fg*cos(a)=u*(m3)*g*cos(a)
4.te Gleichung (m3)*g*sin(a)=u*(m3)*g*cos(a)+(m3)*a+Fs2
Mit diesen 4 Gleichungen kann man die Beschleunigung a=... ausrechnen
Daraus ergibt sich dann der zurückgelegte Weg S(t)=x4=1/2*a*t²
Den Rest schaffst du hoffentlich selber.
Tipp:Setze Zahlenwerte ein,mit denen man gut rechnen kann und überprüfe so deine Formeln.
Kannst auch den Energieerhaltungssatz anwenden.
1) die Masse m hebt sich um 1 m an
2) daraus kannst du dann die Bewegungen der Umlenkrolle,Zylinderrolle und der Masse (m3) berechnen
Energiezustand 1 E1=0 Epot(m)=0 und Ekin=1/2*m*v²=0 weil v=0
Energiezustand 2 E2=Epot(2)=m*g*h → h=1 m
Zylinderrolle E2(z)=m*g*(h1-h2)+1/2*J*w²
h1-h2= Änderung der Höhe der Zylinderrolle
w=Winkelgeschwindigkeit der Zylinderrolle,wenn sie 1 m zurückgelegt hat.
Bei der Masse (m3) kommt noht die Reibarbeit hinzu Wr=Fr*s
Achte auf die Übersetzung an der Umlenkrolle mit R>r
danke wieder mal für deine ausführliche antwort! Jedoch weiß ich wie man die gleichungen etc aufstellt an dem Zylinder gilt der Drallsatz und an den Massen der Impulssatz, an der großen Rolle ist die linke seite gleich 0 weil das masselos ist dementsprechend: S1*r=S2*r etc.
Mein Problem ist es leider wie man die kinematischen zwangsbedingungen aufstellt in teil b)
b) is ja ganz einfach
x4=x1*r/R
Beispiel:wenn R=2 m und r=1 m dann wäre,wenn sich m um 1 m hebt
x4=1 m*1 m/2 m=0,5 m → Masse (m3) würde sich dann nur um 0,5 m bewegen
Umfang vom Kreis U=2*r*pi=d*pi
360°=Vollkreis in grad
1° sind dann U/360°
(a) sind dann U/360°*(a°) → zurückgelegte Strecke wenn(a°) Drehwinkel in grad
2*pi=Vollkreis in rad
1 rad=U/(2*pI)
(a) sind dann U/(2*pi)*(a) mit (a) Winkel in rad
zurückgelegter Weg s=r*phi
Beispiel: r=1 m → Vollkreis U=2*1m*pi=6,283 m
s=1 m ergibt den Drehwinkel phi
s=r*phi
phi=1 m/1 m= 1 rad
Probe: U=6,283 m → 1 rad sind dann 6,283 m/(2*pi)=1 rad
s=0,5 sind dann phi=s/r einen Drehwinkel von phi=0,5 m/1m=0,5 rad
puh mir scheint das sehr kompliziert rüberzukommen :/
Vielen dank für die Antwort, aber ich habe echt kein plan wie die zusammenhänge von x1 und x4 sind. Ich würde einfach sagen x1*r+x4*r