Wie spiegele ich Parabel an y-Achse (10. Klasse)?

Hallo,

wie sieht eine gespiegelte Parabel an der y-Achse aus?

Außerdem muss ich diese Parabel auch mit der x-Achse spiegeln.

Deine Antwort ist sehr geschätzt.

Danke im Voraus!

Answer 1

[ethan227]

Hier sind die Formel, die Du brauchst, um eine Parabel an beiden Achsen zu spiegeln.

Um eine Parabel an die y-Achse zu spiegeln, solltest Du einfach diese Formel nutzen.

Bei einer quadratischen Funktion von

$y\ =\ x^2\ -\ 2x\ +\ 7$ solltest Du einfach den Wert von x hier mit (-x) ersetzen, wovon Du

$y\ =\ \left(-x^2\right)\ -\ 2\left(-x\right)\ +\ 7$ $y\ =\ -x^2\ +\ 2x\ +\ 7$ bekommst.

In diesem Schritt werden wir durch die quadratische Ergänzung prüfen, ob die beide Parabel sich spiegeln.

Für Gleichung I :

$y\ =\ \left(\ x\ -\ 1\right)^2\ +\ 6$ Schnittpunkte : 1, 6

Für Gleichung II :

$y\ =\ -\left(x\ -\ 1\right)^2\ +\ 8$ Schnittpunkte : 1, 8

Für die x-Achse ist es einfach, bzw. die Funktion musst Du einfach durch -1 multiplizieren, um die Gleichung der Spieglung zu bekommen. In dieser Gleichung wäre es

$y\ =\ -x^2\ +\ 2x\ -\ 7$

Hoffentlich könnte ich Dir damit weiterhelfen. :)

Woher ich das weiß: Studium / Ausbildung – Mathematik ist seit langem mein Lieblingsfach.🧮

Answer 2

[Kalkablagerung]

Eine Parabel ist immer achsensymmetrisch zu einer zur y-Achse parallelen Linie. Wenn du also an der y-Achse spiegelst, bedeutet das für die Parabel, dass du diese praktisch nur verschiebst. Beispiel: $f\left(x\right)\ =\ \left(x+1\right)^2\ +\ 2$ Diese Parabel ist um 1 nach links verschoben; also wäre eine an der y-Achse gespiegelte Parabel 1 nach rechts verschoben.

An der x-Achse spiegelt man, indem man das Vorzeichen umdreht. Also alles, was positiv ist, wird negativ gemacht und alles, was negativ ist, wird positiv gemacht. Die Funktion von oben würde dann so aussehen: $fv\left(x\right)\ =\ -\left(\left(x+1\right)^2\ +\ 2\right)$ Also $fv\left(x\right)\ =\ -\left(x+1\right)^2\ -\ 2$ fv ist jetzt einfach mal die an der x-Achse gespiegelte Funktion.

Wenn die Funktion in der Normalform gegeben ist, kannst du diese entweder vorher in die Scheitelpunktform umwandeln oder bei x-Spiegelung alle Vorzeichen umdrehen, bei y-Spiegelung alle x gegen -x tauschen, weil ja alle positiven x gegen negative x getauscht werden (weil die Seiten links und rechts getauscht werden) bei einer Spiegelung der Parabel.

Die Funktionen noch einmal hier visuell:

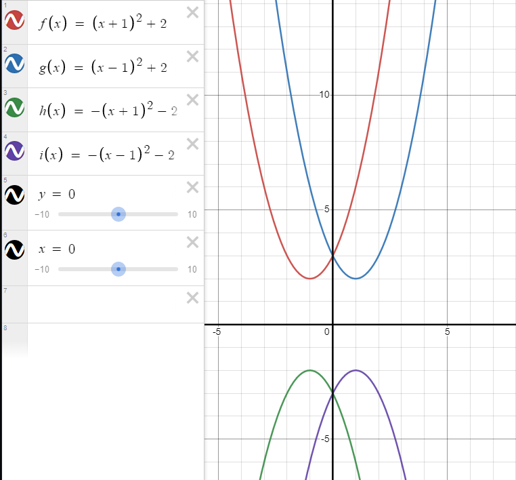
Bei Fragen gerne fragen!

Woher ich das weiß: Hobby – Ich interessiere mich für Mathematik

Answer 3

[Kaenguruh]

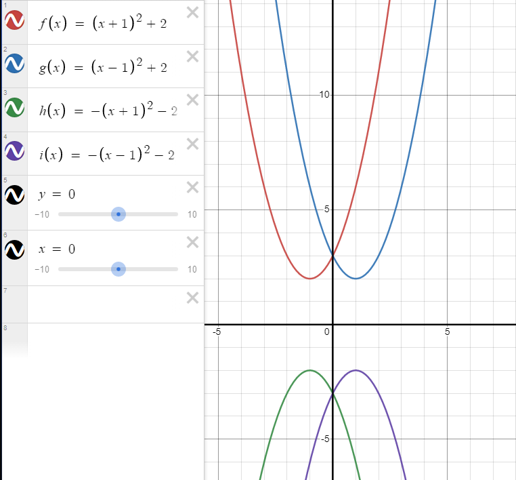
A: Spiegelung an der y-Achse:

Du ersetzt x durch (-x) in der Originalfunktion.

Beispiel: y = 2 x² - 5x. Gespiegelt:

y = 2 (-x)² - 5 (-x) = 2x² + 5x

B: Spiegelung an der x-Achse

Du multiplizierst die Funktion mit (-1)

Beispiel: y = 2x² - 5x. Gespiegelt:

y = - 2x² + 5x