Wie sieht ein 4-dimensionaler Hyperwürfel genau aus?
Ich habe hier zwei verschiedene Bilder von Würfeln der vierten Dimension. Welches von beiden stimmt jetzt.
9 Antworten
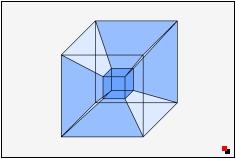
Beide Bilder sind richtig. Das linke zeigt den 4D-Würfel in der Zentralprojektion, das rechte in der Parallelprojektion. Die, wie ein 4D-Würfel aussieht, kann nicht beantwortet werdem, da das Anschauungsvermögen des Menschen auf 3 Dimensionen beschränkt sind. Die geometrischen Eigenschaften des 4D-Würfels lassen sich natürlich trotzdem herleiten.
Also mal Butter bei die Fisch:
Die Darstellungen sind 2-dimensional, von (mehreren) 3-dimensionalen Würfeln. Als 4. Dimension wird, z.B. bei Gravitationsbetrachtungen, die Zeit gewählt und anschließend der 3-dimensionale Raum 2-dimensional dargestellt. Zu Deiner Frage fehlt das betreffende Bezugsystem, folglich ist die Antwort:
Keines der Bilder!
Das ist mir sehr bewusst, aber nicht direkter Hintergrund meiner Bemerkung. Es fehlt die Bezugsbedingung zur 4. Dimension! ;-)
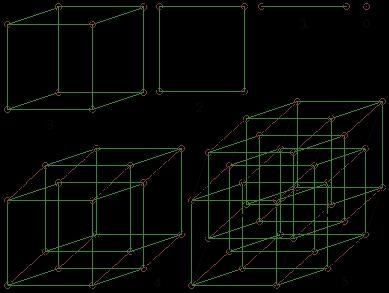
Das Quadrat hat 4 Ecken und 4 Kanten. Der Würfel hat 8 Ecken und 12 Kanten. Der 4-dimensionale Hyperperwürfel 16 Ecken und 32 Kanten. Im Bild mit schwarzem Hintergrund siehst Du zu allem Überfluss auch noch den 5-dimensionalen Hyperwürfel mit 32 Ecken und ich weiss nicht wieviel Kanten. Alles in Parallelprojektion.
Das blaue Bild zeigt, wenn Du genau hinschaust, ebenfalls 16 Ecken und 32 Kanten. Nur wird hier eine Zentralprojektion angewendet. Dadurch wird eine der 4 Dimensionen stark verjüngt.
Also sind beide Bilder richtig. Zähle die Ecken und Kanten nach!
Ich halte das schwarze Bild für die korrekte Projektion.
Warum: Wenn Du einen 3D-Kubus (Würfel) auf ein Blatt Papier projizierst, dann bekommst Du zwei ineinander verschobene 2D-Kuben (=Quadrate!)
Ein auf die drei Dimensionen projizierter Hyperwürfel müsste meiner Meinung nach zwei ineinander geschobene 3-D Würfel ergeben.
(Diese Begründung ist nicht mathematisch exkat, sondern gibt mein mathematisches "Bauchgefühl" wieder).
Da wir nicht 4-dimensional sehen können, können wir nur Projektionen eines Hyperwürfels sehen. Und die Projektion eines Hyperwürfels sieht eben aus wie ein 3-dimensionaler Würfel.
Das ist keine Gravitationsbetrachtung.