Wie liest man am besten eine Parabel ab?
Also zb. Wenn man jetzt eins nach rechts geht und man solange nach oben gehen muss bis man die Parabel berührt...aber was ist wenn es ungenau ist bzw.das da jetzt 1,6 kommt...Kann man das auch anders machen?Also zb.das man zwei nach rechts geht und solange nach oben bis man den Graphen berührt aber es dann im Bruch angibt?
Oder kann mir da jemand helfen bitte?
4 Antworten
Wenn man jetzt eins nach rechts geht
Eine Einheit nach rechts? Was soll das bringen?
solange nach oben gehen muss bis man die Parabel berührt
Das klingt schon vernünftiger, bloß kann die Parabel nach unten geöffnet sein, dann musst du nach unten gehen.
Am besten du zeichnest eine Parallele zur x-Achse, so dass sie die die Parabel genau an ihrem Scheitel berührt. Den Schnittpunkt der Geraden mit der y-Achse nennen wir y0.
Dann zeichnest du eine Parallele zur y-Achse, die durch diesen Berührungspunkt geht. Den Schnittpunkt der Geraden mit der x-Achse nennen wir x0.
Dann lautet die Funktion der Parabel:
f(x) = (x-x0)² + y0
Abzählen geht nicht ohne Kästchen.
Wenn das Ablesen der Bestimmung von a ( y = a*x²) dient muss man schauen ob man schon bei x = 1 oder x = 2 zum Ziel kommt.
hier
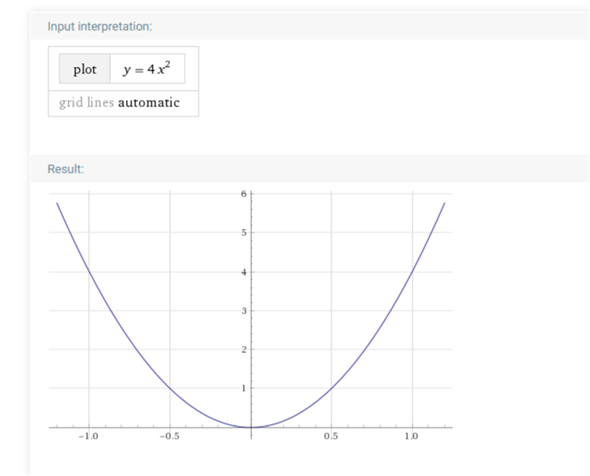
funktioniert es ganz gut : zu x = 1 gehört f(x) = 4 , daher ist a = 4
bei a = 1.6 ist es ungenau ........ besser geht es nicht
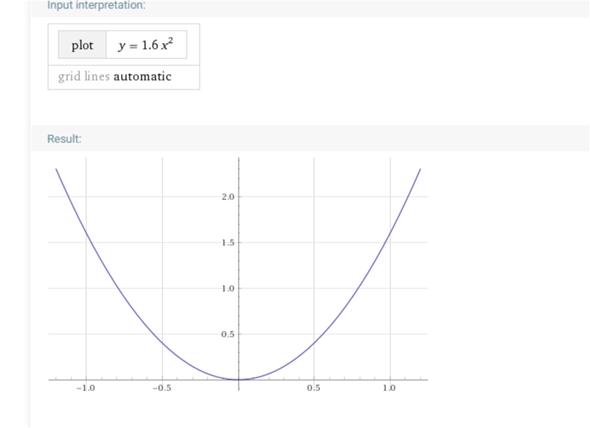
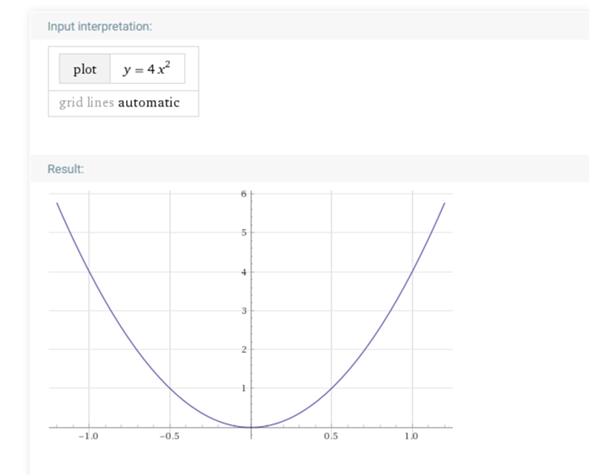
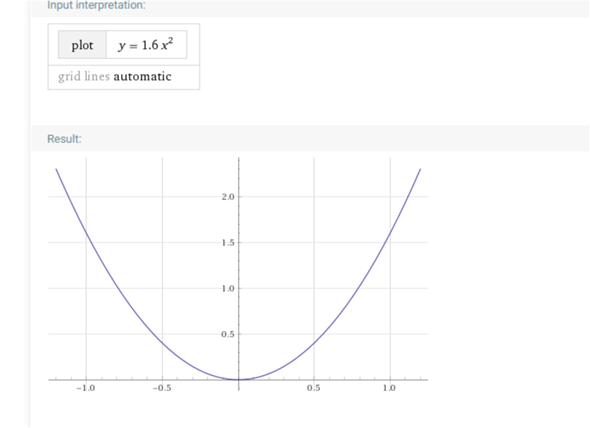
allgemeine Form y=f(x)=a2*x²+a1*x+ao
Scheitelpunktform y=f(x)=a2*(x-xs)²+ys
Scheitelpunkt Ps(xs/ys) mit xs=-(a1)/(2*a2) und ys=-(a1)²/(4*a2)+ao
am besten den Scheitelpunkt ablesen xs und ys und in die Scheitelpunktform einsetzen.
Allgemein liest man ganze Werte ab (ganze Zahlen für x=... und y=..)
Umwandlung in die allgemeine Form mit den binomischen Formeln
1) (x+b)²=x²+2*b*x+b²
2) (x-b)²=x²-2*b*x+b²
Ein Bruch kann auch eine Dezimalzahl sein
Jede rationale Zahl kann als Bruch von ganzen Zahlen dargestellt werden.