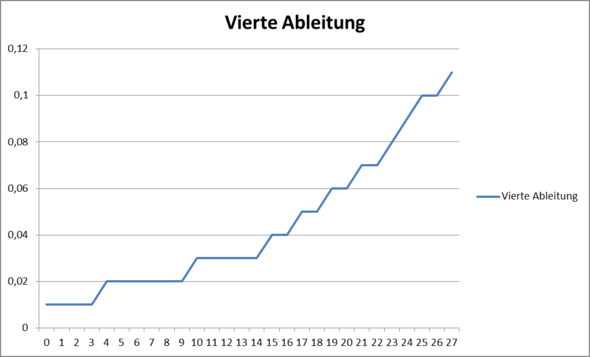
Wie kann man dieses Diagramm beschreiben?
Kann mir bitte jemand sagen, was das für eine Funktion ist: eine lineare, exponentiale.... Oder keins davon?
Der Funktionsterm zum Diagramm ist folgende:
K(t) = 200 * ln(1,09)^4 * 1,09^t
Ignoriert bitte die Bildüberschrift!
Danke im Voraus!
lGSuppe
1 Antwort
Die Funktion selber ist eine Exponentialfunktion.
200 * ln(1,09)^4 ist eine Konstante (der "Startwert"), 1,09 ist der Wachstumsfaktor.
Problem: Der Graph der Funktion K ist eine glatte Kurve, die langsam aber sicher immer steiler wird.
Im Diagramm selber ist aber ein Graph dargestellt, der ja stückweise sogar konstant bleibt. K könnte allerdings eine Näherungsfunktion zum dargestellten Graphen sein.
Ich verstehe das so:
Du hast eine Funktion k(t) = 200 · 1,09^t gegeben, die den Verlauf eines Kapitals von 200 € im Laufe der Zeit angibt, welches mit 9 % verzinseszinst wird.
Die von Dir beschriebene Funktion K(t) stellt die vierte Ableitung von k dar. Soweit alles okay. Dabei gilt: K(t) = ln(1,09)^4 · k(t).
Nun kommt die Frage: Gehst Du von einer stetigen Verzinsung des Kapitals aus (dann sind für t alle reellen Zahlen zugelassen; in der Mathematik der Standardfall; ID = IR) oder vermehrt sich Dein Kapital sprunghaft immer am 31.12. eines Jahres (dann wären nur ganze/natürliche Zahlen für t zugelassen; also ID = IN)?
Im ersten Fall sind beide Graphen (also der von k und der von K) glatte Kurven, wobei die von K gegenüber der von k (extrem) gestaucht ist.
Im zweiten Fall dürften die Graphen nur aus einzelnen Punkten bestehen. Evtl. könnte man den Graphen von k noch als "Treppe" zeichnen, bei der das Kapital im Laufe des Jahres unverändert bleibt. Das würde dann evtl. auf Deinen Graphen von K führen. (Wobei der Graph eigentlich für natürliche Zahlen positive Werte hätte, ansonsten immer den Wert null haben müsste (da das Kapital sich ja immer nur zu Jahresende verändert).
Soweit meine mathematische Meinung :-)
Einen speziellen Namen für den Graphen kenne ich übrigens nicht - gibt es den?
ja, dargestellt ist eine jährliche Verzinsung im Jahr. Aber es geht hier nicht um das Endkapital, sondern um die Zinsen selbst. Die vierte Ableitung stellt die Steilheit der Steilheit der Zinsen dar. Ich habe das nicht ganz verstanden mit "Steilheit der Steilheit". Hast du da eine Ahnung? Wenn ja, vielen Dank im Voraus :)
Wenn man "Steilheit" mit "Wachstum" übersetzt, wird's wohl etwas deutlicher.
Die erste Ableitung gibt das Wachstums des Kapitals an, also die Zinsen.
Die zweite Ableitung gibt das Wachstum des Wachstum des Kapitals, also das Wachstum der Zinsen an: um wie viel Euro steigen die Zinsen von Jahr zu Jahr an?
Die dritte Ableitung... - da wird es schon schwieriger zu erklären. Aber vielleicht ist das Prinzip deutlich geworden.
1) Also ist die vierte Ableitung: Das Wachstum des Wachstums des Wachstums des Wachstums des Kapitals? Wow hahahaha das ist so gar nicht verwirrend.
Ich muss darüber eine Präsentation halten und wollte das deshalb mit einem Diagramm darstellen. Mit der vierten Ableitung kann ich ja schön sehen, wie die Zinsen immer schneller ansteigen (da die Linien, wo m=0 ist, immer kürzer werden und zwischen den Jahren der Anstieg sehr steil ist, ab dem 23. Jahr folgt sogar ein kurzer linearer Anstieg).
2)Aber was kann ich mit der dritten Ableitung erkennen? Ist sie überhaupt wichtig (praktisch gesehen)?
3)Ist das obige Diagramm streng genommen überhaupt noch ein Graph? (Was ich auch komisch finde ist, dass die Ableitung eigentlich von der Formel her eine exponentielle Funktion ist, mit dem hoch 4, aber im Diagramm keine exponentielle Funktion zu erkennen ist).
4)Und was mir auch aufgefallen ist, ist dass die erste Ableitung zum Beispiel die Differenz zweier ursprünglicher Funktionen ist, nur dass der Wert näherungsweise angegeben wird. Ist das regulär bzw. ist das bei allen Ableitungen von Funktionen so oder stellt die Zinseszinsformel eine Ausnahme dar? Oder hat das etwas damit zu tun, dass die Zinseszinsformel eine geometrische Folge ist?
sorry, dass ich so viele Fragen stelle!!!!!!!!!!!
Hey! Danke für deine Antwort.
Genau, diese Formel ist die vierte Ableitung der Zinseszinsformel. Die vierte Ableitung stellt den Anstieg der Steilheit der Steilheit der Zinsen da. Nähert sie sich dann wirklich der Funktion? Wenn die Stammfunktion (also die Zinseszinsformel) den Anstieg des Endkapitals beschreibt, inwiefern soll sich die vierte Ableitung dieser dann nähern? Gibt es für mein Diagramm einen konkreten Namen?