Lineare Funktionen (9 Klasse)?
Hey Leute,
Ich habe Probleme mit dem Thema: lineare Funktionen bzw. Wie beschreibe ich die Formel mx+b in einem Koordinatensystem mit Funktionen.
Eine kurze verständliche Erklärung über dieses Thema würde mich sehr freuen.
Bitte um Rückmeldung.
3 Antworten
Allgemeine Formel: f (x)=mx+b
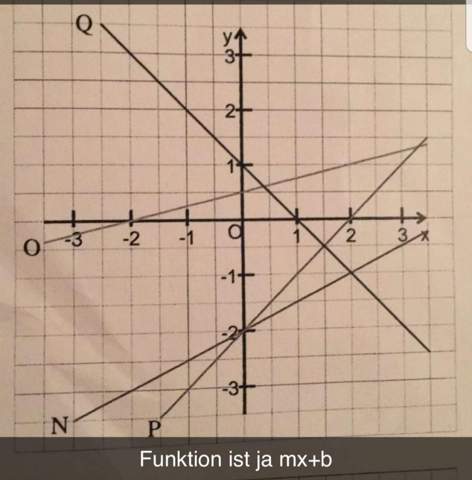
Nehmen wir als Beispiel Q:
b= der Punkt, der die y-Achse schneidet
= 1
m= Steigung eines Graphen
Hilfsmittel: Steigungsdreieck: y/x (Bruch)
Bei Q suchst du dir einen gut ablesbaren Punkt, z.B. P (0|1), von dort suchst du dir einen weiteren gut ablesbaren Punkt, zB. G (1|0).
Jetzt zeichnest du dir das Steigungsdreieck ein: Du gehst eine Einheit nach unten und eine nach rechts, sodass ein Dreieck ensteht. Du zählst dabei immer, wie viele Einheiten du gewandert bist. Bei meinen augewählten Punkten: 1/1 (Bruch). Jetzt weißt du, dass m=1 ist.
Abschließend guckst du dir die Gerade an, ob sie fallend oder steigend ist. Bei fallend musst du ein - (Minus) vor das m schreiben.
m=-1
Wenn der Graph aber steigend ist, musst du das Steigungsdreieck nach oben und nach rechts einzeichnen.
Jetzt setzt du dein Erebnis in dir oben gennante Formel: f(x)=-1x+1
b ist der y-Achsenabschnitt, also der y-Wert, bei dem der Graph der Funktion die y-Achse schneidet.
m ist die Steigung. Diese kann man sich durch ein Steigungsdreieck veranschaulichen. Geht man eine Einheit mach rechts, so geht man m Einheiten nach oben bzw. bei negativem m entsprechend nach unten.
Und wie müsste ich dann mx+b beschriften?
Danke für ihre Antwort
allgemeine Form y=f(x)=m*x+b
einfachste Form y=f(x)=m*x alle Graphen gehen durch den Ursprung P(0/0)
Sekantensteigung m=(y2-y1)/(x2-x1) mit x2>x1 sind 2 Punkte P1(x1/y1) und P2(x2/y2)
Die Sekante ist eine Gerade durch 2 Punkte.
Hier Infos per Bild,was du mit deinem Bildprogramm vergrößern kannst.

