Wie kann ich diese Mathe-Aufgabe lösen (Winkel)?
Hallo, ich komme bei dieser Aufgabe einfach nicht weiter. Kann mir jemand helfen?

2 Antworten
Aufgabe 22
γ13 = arctan(a1 / b1)
γ13 = arctan(6 / 4)
γ13 = 56,309932°
---
a = Wurzel(a1² + b1²)
a = Wurzel(5^2 + 4^2)
a = 7,211103 km
---
γ14 = 90 - α1
γ14 = 90 - 8
γ14 = 82°
---
γ = 180 - γ13 - γ14
γ = 180 - 56,309932 - 82
γ = 41,690068°
---
β = 180 - α - γ
β = 180 - 67 - 41,690068
β = 71,309932°
---
Geg.: a=7,211103 ; α=67°
β=71,309932 ; γ=41,690068
b = a / SIN(α) * SIN(β)
b = 7,2111 / SIN(67) * SIN(71,30993)
b = 7,420744 km
---
c = a / SIN(α) * SIN(γ)
c = 7,211103 / SIN(67) * SIN(41,690068)
c = 5,210305 km
---
x3 = c * cos(α3)
x3 = 5,210305 * cos(15)
x3 = 5,032768 km
---
y3 = c * sin(α3)
y3 = 5,210305 * sin(15)
y3 = 1,348526 km
---
x = x2 - x3
x = 7 - 5,032768
x = 1,967232 km
---
y = y2 - y3
y = 4 - 1,348526
y = 2,651474 km
Die Position des Schiffes ist ( 1,967|2,651 )
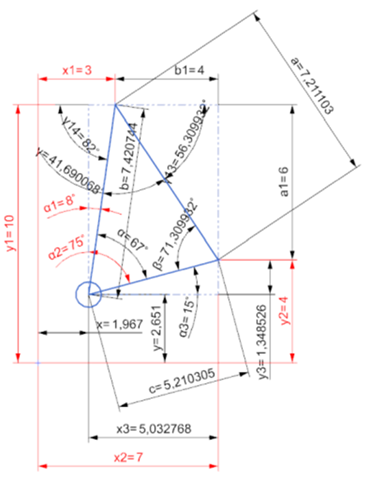
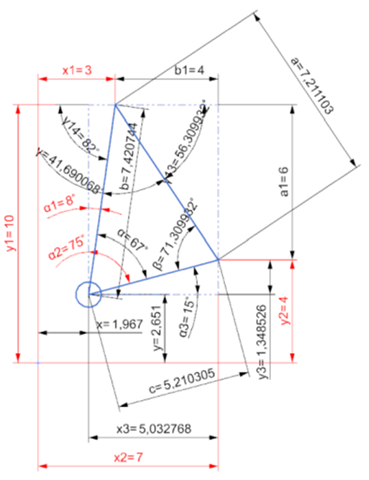
Die Aufgabe stammt aus einem Buch der 7. Klasse. Man kann sie zwar sicher so lösen, aber es muss doch einen anderen Weg geben.
Schiff = M ; Suderogsand = S , Westerheversand = W
Winkel aus Koordinatendifferenzen:
arctan(6 / 4) = 56,30993° ; arctan(4 / 6) = 33,69007°
Dreieckswinkel Dreieck MSW aus gegebenen Richtungswinkeln:
Winkel MSW = 180° + 8° - 56,30993° - 90° = 41,69007°
Winkel SWM = 360° - (75° + 180° + 33,69007°) = 71,30993°
Winkel WMS = 75° - 8° = 67°
41,69007° + 71,30993° + 67° = 180°
Strecke s_S,W = √52 = 7,2111
Strecke s_M,W = 5,10913
Strecke s_M,S = 7,27664
Damit sind alle Winkel und Strecken bekannt und die Koordinaten von M (Schiff) können mittels Winkelfunktion und der Koordinaten von S und W bestimmt werden.
x_M = 1,967
y_M = 2,651