Wie integriert man von x bis unendlich?
Hallo!
Ich würde gerne die Gammafunktion lernen. Aber dafür muss ich wissen, wie man von 0 bis unendlich integriert. Wie macht man das?
Die Gammafunktion lautet ja: Γ(x) = (Integral von 0 bis unendlich) t^(x-1)*e^(-t) dt
Aber wie integriere ich das von 0 bis unendlich?
Angenommen, Ich würde das machen:
∞^(x-1)*e^(-x) - 0^(x-1)*e^(0) = ∞^(x-1)*e^(-x) - 1 =? ∞ - 1 = ∞
Das würde heißen, dass x! = ∞. Aber das stimmt offensichtlich nicht:
1! = 1
2! = 2*1 = 2
3! = 3*2*1 = 6
4!=4*3*2*1=24
...
Wie integriere ich von 0 bis ∞?
Und wie mache ich das auf dem TI-84 Taschenrechner?
Ich sehe kein Unendlichkeitszeichen.
∞^(x-1)*e^(-x) - 0^(x-1)*e^(0) = ∞^(x-1)*e^(-x) - 1 =? ∞ - 1 = ∞
??? ist das nun ernst gemeint ???
Ja.
Ich glaube nämlich nicht, dass das richtig ist. Deshalb frage ich.
3 Antworten
Angenommen, Ich würde das machen:
∞^(x-1)*e^(-x) - 0^(x-1)*e^(0) = ∞^(x-1)*e^(-x) - 1 =? ∞ - 1 = ∞
Angenommen du machst Unsinn, dann kommt Unsinn raus, korrekt.
Bevor du dich mit der Gamma-Funktion befasst, solltest du erstmal lernen Wie Integration funktioniert (≠ einfach einen kurze Text lesen, du musst es erst richtig verstehen)
Erst wenn du es verstanden hast, solltest du dich erst mit der Gamma-Funktion beschäftigen (und die Funktion wird in jedem ordentlicen Analysis Buch (auf Uni Niveau) behandelt)
Und BTW:
Wenn eine Funktion über ein Integral definiert wird, und dann noch einen Extra Namen bekommt, ist das oft nicht ohne Grund. Die Gamma-Funktion ist per Hand nicht so einfach bis gar nicht berechenbar.
Zumindest wird die Eigenschaft Gamma(n+1)=n! Für alle natürlichen Zahlen durch Induktion gezeigt, und nicht, indem man einfach das Integral für n bestimmt.
∞^(x-1)*e^(-x)
Da ist ein Abschreibfehler. Es hätte e ^ -t sein sollen.
Und da e ^ -t bei großen t gegen Unendlich geht, haben wir eine Kurve, die irgendwann sehr schnell gegen die X-Achse fällt, und damit hat das Integral einen endlichen Wert.
Nochmal anders betrachtet:
t^(x-1)*e^(-t)
Dazu müssten wir eine Aufleitung (Gegenteil von Ableitung) finden. Die erhalten wir nicht so einfach, sonst hätte man nämlich die Gammafunktion anders definiert. Dennoch...wenn man in die Grundfunktion t^(x-1)*e^(-t) den Wert ∞ direkt einsetzt, erhalten wir ∞^(x-1)*e^(-∞)
Wir erhalten hier ein unbestimmtes Produkt... Unendlich mal Null ... das jeden beliebigen Wert haben könnte, was uns daher nichts nützt. Und genau dafür gibt es die Limes-Bestimmung, die für beliebig große t einen Grenzwert sucht, der hier 0 ist. Anschaulich kann man sich vorstellen, dass t ^ x langsamer wächst, als e ^ t fällt, und somit bei großen Zahlen immer die Exponentialfunktion "gewinnt". Die Funktionskurve nähert sich also im Unendlichen asymptotisch (und sehr schnell) der X-Achse an.
Auch zum Themenbereich Gamma-Funktion:
Ein lustiges Video über die Stirling-Formel, die die Fakultät approximiert und ihre Herleitung.
Übrigens, ist zu beachten, dass es zwei Funktionen gibt, die die Fakultät approximieren.
Die seltener verwendete Gauss'sche Produkt-Funktion PI(n) interpoliert n!
während für die Gamma-Funktion gilt: Gamma(n+1) = n!
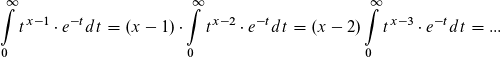
Anders ausgedrückt:
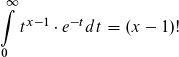
Achtung! Ich habe mir gerade nur ein 13-Minuten-Video auf YouTube reingezogen, also Angaben ohne Gewähr!
Aber wie eine Funktion mit der Grenze Unendlich "wirklich" integriert wird, zeige ich am folgendes Beispiel:
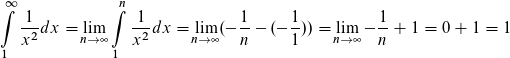
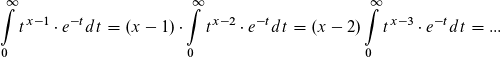
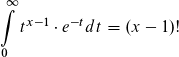
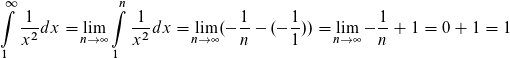
Vielen Dank!