Wie geht es richtig?
2 Antworten
Mach das einfach mit der linear Faktorzerlegung.
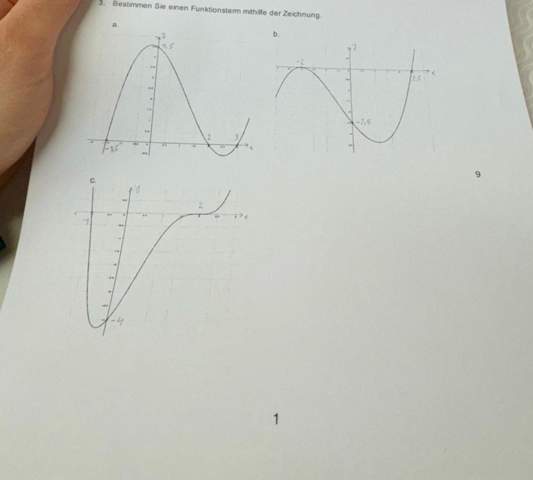
Schau, wo der Graph die x-Achse schneidet. Du nimmst diese Stelle und schreibst sie in folgender Schreibweise: (x - Stelle), je nachdem, ob an dieser Stelle die x-Achse geschnitten, berührt oder der Sattelpunkt draufliegt, kommt eine andere Potenz hinter die Klammer.
Hier ein Beispiel zum ersten Graphen von dir:
Nullstellen bei x = -1,5, x = 2 und x = 3 (wenn ich es richtig sehe).
Also hast du:
f(x) = a(x + 1,5)(x - 2)(x - 3)
Das a ist dein Streckfaktor, den musst du noch berechnen. Dazu nimmst du irgendeinen Punkt aus dem Graphen und setzt ihn in deine Gleichung ein. (Nur die Punkte, wo der Graph die x-Achse schneidet, darfst du nicht nehmen!). Dann löse nach a auf und das wars.
Bei b):
f(x) = a(x + 2)^2(x - 2,5)
Hoch 2, weil der Graph bei x = -2 die x-Achse berührt. Bei Sattelstellen hast du entsprechend x^3.
Dann wieder einen Punkt aussuchen und a berechnen.
ich hoffe, ich konnte die Stellen richtig ablesen, schwer zu erkennen
Grad der Funktion ermitteln: Anzahl der Extrempunkte + 1 = Grad der Funktion
pro unbekanntem Koeffizient suchst du dir einen ablesbaren Punkt raus und bildest damit je eine Gleichung für das LGS, danach löst du es nach den Parametern auf
Funktionsgleichung aufschreiben
fertig
Und was, wenn da ein Sattelpunkt ist? Was machst du dann?
Ach was geht deutlich leichter mit linar faktoren