Wie errechnet man die Lösungsmenge aus 14x^2 =84x?
Entschuldigung, dass ich heute so viel Frage. Zur Aufgabe : Durch ausprobieren finde ich zwar die Lösung heraus, doch wie errechnet man sich die Lösung richtig?
Das gibt in der Arbeit ja bekanntlich die meisten Punkte.
4 Antworten
Du kannst die Gleichung so umstellen:
14x² = 84x | -84x
14x² - 84x = 0 | : 14
x² -6 x = 0
Und jetzt x ausklammern:
x(x-6) = 0
Ein Produkt ist dann 0, wenn einer der Faktoren =0 ist. Die Gleichung ist also erfüllt, wenn
x = 0 oder (x-6) = 0.
D. h. die erste Lösung ist x = 0. Die zweite ergibt sich aus
x -6= 0 | +6
x = 6.
Die Lösungsmenge der ursprünglichen Gleichung ist also {0 ;6}.
Du kannst es auch anders begründen:
14x² = 84x
Da auf beiden Seiten x ein Faktor ist, ist x=0 auf jeden Fall eine Lösung. Sei nun x ungleich 0, dann kann ich durch x teilen:
14x² = 84x | :x
14x = 84 | :14
x = 6.
Damit ist x =6 die zweite Lösung.
Stelle die Gleichung zuerst so um, dass sie der Form x² + p*x + q = 0 entspricht. Also mit deinem Beispiel:
14x² = 84x
<=> 14x² - 84x = 0
<=> x² - 6x = 0
Dein p ist also -6 und dein q ist 0
Jetzt benutzt du die pq-Formel, die allgemein so aussieht (sqrt steht für die Wurzel):
x_1 = -p/2 + sqrt( (p/2)² - q)
x_2 = -p/2 - sqrt( (p/2)² - q)
Wenn du nun p = -6 und q = 0 entsprechend einsetzt erhältst du als Lösung x_1 = 6 und x_2 = 0
Es ist einfach völlig unsinnig, die pq-Formel in einem Fall zu verwenden, in dem p oder q gleich Null sind. Da ist der direkte Weg einfacher. Natürlich geht es - es zeigt aber nur, dass man das mit den quadratischen Gleichungen nur sehr oberflächlich verstanden hat.
Ist nämlich p = 0, so hat man
x² + q = 0, dann sind +- Wurzel(-q) die beiden Lösungen (falls man nur im Reellen rechnet, existieren die nur für -q >= 0).
Ist (wie hier) q = 0, so hat man
x² + px = 0 und man kann ausklammern: x (x+p) = 0 und man sieht, dass 0 und - p die beiden Lösungen sind.
Die pq-Formel ist dafür da, den schwierigen Fall schnell zu lösen, nicht die einfachen Fälle, das ist ein völlig unnötiger Umweg.
14x^2=84x |-84x
14x^2 -84x +0 = 0
P,Q-Formel
x^2+px+q=0
x1,2= -p/2 +-√(p^2/4-q)
x1,2= 84/2 +-√(84^2/4-0)
x1 und x2 ausrechnen
L={} bestimmen
Denk dran das das L bei der L={} zwei senkrechte Striche hat
:)
da bin ich anderer Meinung. es ist besser jemanden nicht zu verunsichern. Mir ist aber auch klar das man anders mehr Zeit hat. Das ist aber nur der Fall wenn man das gut kann, sonst ist das verwirrend.
Nein. Gerade in der Schule soll man eben begreifen, wann man die Formel anwenden soll und wann nicht. Das ist dann der Unterschied zwischen einem Schüler, der stur die Formeln kann und einem, der wirklich gut in Mathe ist. Der eine braucht dann in der Arbeit lange, weil der diesen Umweg macht (und beschwert sich hinterher, dass so wenig Zeit war), der andere sieht den Lösungsweg sofort. Dieses sture "Ich-kann-ja-die-Formel-anwenden-also-hab-ich-alles-verstanden" ist dermaßen hinderlich, wenn es dann später mal schwieriger wird.
Es gibt da prinzipiell die Mitternachtsformel um quadratische Gleichungen zu lösen aber in diesem Fall ist es auch ohne gut lösbar.
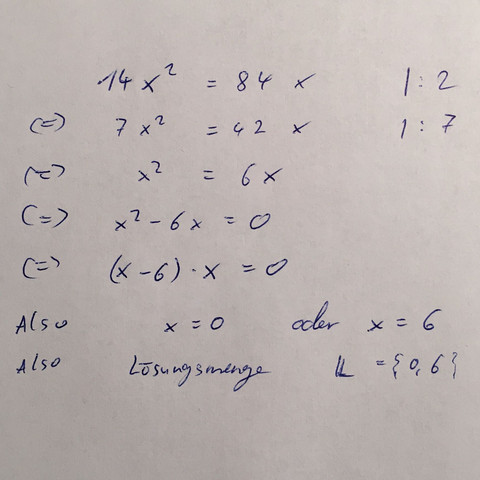
Klasse Antwort! Besser geht es nicht :)
Den Stern hast du SICHER! :)
naja, so macht man es in der Schule immer und wenn schon gefragt wird wie es geht, dann ist es doch besser bei einer Variante bleiben zu können :) aber ja hast schon recht