Wie berechnet man die Induktivität einer Spule?
In eine Zylinderspule der Länge l mit N Windungen und einer Querschnittsfläche A wird ein zylindrischer ferromagnetischer Kern der Länge l/2 eingeführt.
Berechnen Sie die Induktivität der neuen Spule, wenn die Induktivität in Luft L(0) beträgt
Könnte mir die Aufgabe jemand erklären? Ich kann es mir zwar bildlich vorstellen, aber wie gehe ich hier rechnerisch vor?
Danke!
3 Antworten
Ich weiß nicht, welche "Formeln" ihr kennengelernt habt, aber wenn man das Feldlinienbild ansieht, wird der Weg klar, wie man das näherungsweise für eine lange Spule berechnen kann.
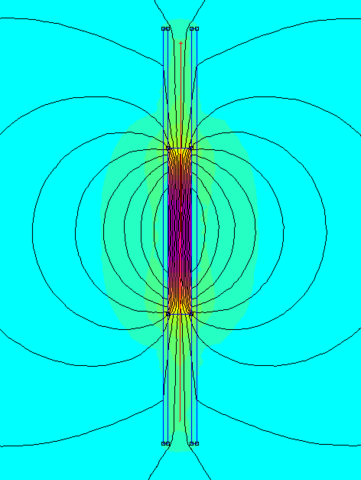
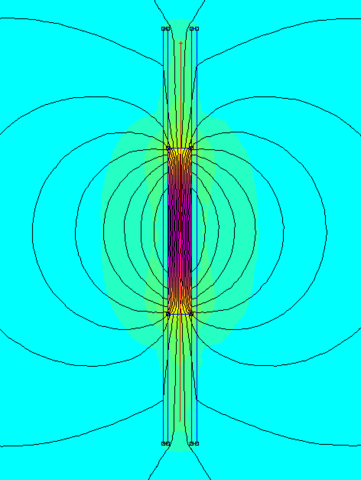
Die Berechnung (Spulenlänge L=8cm, I=1A, N=100) habe ich mit einem FE-Tool gemacht, die Permebilität des Kerns ist 10000.
Hier gibt es zwei Bereiche (ich habe es ungefähr gedrittelt statt halbiert weil mir das abmessen zu blöd war - tut aber nichts zur Sache):
- oben und unten ohne Kern (2 mal l/3)
- in der Mitte der Kern (l/3)
Das Magnetfeld H ist im Kern fast null - klar.
Dann muss aber aufgrund des Ampere'schen Gesetzes auf der Mittelachse
sein.
Hm ist das mittlere Feld auf der verbliebenen Länge 2/3*l
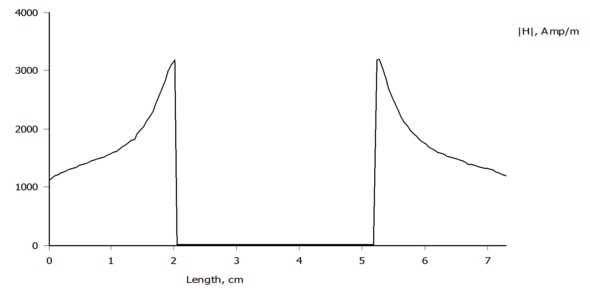
Das kommt bei meiner Simulation ziemlich gut hin. Der teheoretische Wert für Hm müsste bei 1875A/m sein - stimmt also sehr gut (die x-Achse ist der rote Strich in der oberen Zeichnung).
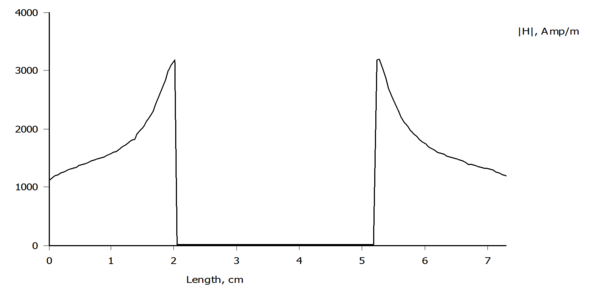
Somit ist klar, welchen Beitrag die oberen und unteren Teile zur Induktivität beisteuern und dieser Teil ist abgehakt.
Bleibt der mittlere Teil: Dort dringen Feldlinien seitlich ein, da es ein Dipolfeld ist.
Es gibt Formeln für kurze Spulen, die mit einem Kern gegebener Permeabilität befüllt sind. Diese kann man hier anwenden auf den Mittelteil. Man macht dabei keinen großen Fehler wenn der Rest der Spule oben und unten dabei ist, da das Eindringen der Feldlinien weitgehend nur in der Nähe der Pole geschieht und man daher bei ausreichendem Verhältnis Länge/Durchmesser diesen Teil vernachlässigen darf. Man sieht das auch recht gut am Bild.
Somit ist die Induktivität die Summe aus
- oberen+unteren Teil mit mittlerem Feld Hm
- und dem Mittelteil der Länge l/3, für welchen es eine Formel gibt.
Das alles ist zwar nicht exakt und etwas krückenhaft, liefert aber glaube ich brauchbare Ergebnisse. Man ist von einer analytisch exakten Berechnung natürlich Lichtjahre entfernt...
Das auf die gewünschte Teilung 1:2 anzuwenden sollte nicht schwer fallen.
Danke für den Stern. Mich würde die Lösung aus der Sicht des Dozenten dennoch interessieren. Kannst Du mich am Laufenden halten?
L = mhy_0 * mhy_r *n²/l dürfte dir bekannt sein....wie man damit umgeht, dass mhy_r hier nicht überall gleich ist, weiß ich nicht genau...und wieso wird die Spule neu? wird sie halbiert?
PS: mhy_r von Luft ist eins....wie kann die Induktivität dann 0 sein? hast du ein Bild der Aufgabe?
Kompliziert wird es vor allem deswegen, weil das Feld außerhalb des magnetisierten Kerns Dipolcharakter hat und somit nicht homogen ist. Das kann man auch analytisch lösen, aber es muss, um den Fluss zu erhalten, über das äußere Dipolfeld integriert werden. Ich glaube, diese Aufgabe hat sich jemand ausgedacht, der selbst nur "Halbwissen" hat - anders kann ich mir es nicht vorstellen.
Naja, der Herr, der die Aufgabe gestellt hat, ist immerhin Professor der Physik
Korrekt und das sogar für Physik II, daher gehe ich davon aus, dass sie tatsächlich so komplex zu lösen ist, wie du angenommen hast. Dennoch fehlt jedem in unserer Lerngruppe jeglicher Ansatz. Insbesondere dass berechnet werden soll, verwirrt uns, entsprechend müsste alles über Konstanten machbar sein, auch das Physikerboard konnte uns nicht helfen, da hieß es schlicht, dass die Aufgabe zu schlampig formuliert sei, um sie zu lösen - für uns unbefriedigend, da ein wissenschaftlicher Mitarbeiter des Professors die Lösbarkeit garantiert hat, wohingegen ein Doktorand ebenfalls keinen Ansatz fand. Alles sehr suspekt...
Ich habe nun die offizielle Antwort:
L(0)=(mhy(0) * N² *A) / (l/2)
L(0(1))=(mhy(0) + mhy(r) * N² * A) / (l/2)
L(0)=L(0)+L(0(1))
L(0)=2* (mhy(0) * mhy(r) * N² * A)/l + (mhy(0) * N² * A) / 2
L(0)=2/L(0) + 2 * mhy(r) * L (0)
Danke - ja, dann ist es wie ich vermutet und oben beschrieben habe:
Bei der Induktivität der mit Kern gefüllten Spule mach man (wie gesagt) einen kleinen Fehler, der aber nicht sehr ins Gewicht fällt. Mehr als eine Milchmädchenrechnung ist das ntürlich nicht - aber für die Abschätzung ist es ausreichend. Ich schätze dass das auf 10% genau hinkommen wird.
Die Formel ist mir bekannt, ja. Das oben ist der Originaltext, ein Bild gibt es dazu nicht, hier ein Screenshot der Aufgabe:
Wie füge ich hier Bilder ein? Finde keinen entsprechenden Button, daher so:
https://abload.de/image.php?img=screenshot_2018-09-14ojewt.png