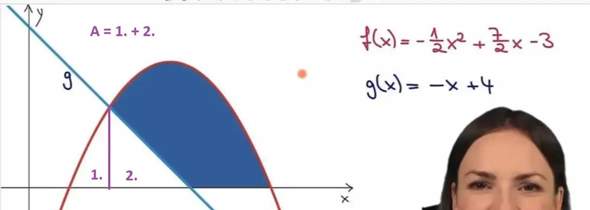
Wie berechne ich die weiße Fläche über der x Achse aber unter der Parabel?

2 Antworten
Hallo.
Das ist eine Zerstückelungsaufgabe. Erst berechnest du das Integral von der Parabel bis zum Schnittpunkt mit der Funktion g(x) und addierst dazu das Integral von g(x) vom Schnittpunkt mit f(x) bis zum Schnittpunkt mit der x-Achse.

In dem konkreten Beispiel berechnen wir also erstmal den Schnittpunkt von f(x) und g(x):
f(x) = g(x)
(-1/2)x² + (7/2)x - 3 = -x + 4
(-1/2)x² + (9/2)x - 7 = 0
x² - 9x + 14 = 0
...............
x(1,2) = 4,5 +- Wurzel(81/4 - 14)
x(1,2) = 4,5 +- 2,5
x = [8; 2]
Der gesuchte Schnittpunkt liegt also bei x=2. Nun noch der Schnittpunkt von g(x) mit der x-Achse:
g(x) = 0
-x + 4 = 0
x = 4
Jetzt noch die vordere Nullstelle der Parabel:
f(x) = 0
(-1/2)x² + (7/2)x - 3 = 0
x² - 7x + 6 = 0
...........
x(1,2) = 3,5 +- Wurzel(49/4 - 6)
x(1,2) = 3,5 +- 2,5
x = [6; 1]
Also berechnen wir den Flächeninhalt der Parabel von x=1 bis x=2 und danach den Flächeninhalt von der Funktion g(x) von x=2 bis x=4.
Was müssen wir dafür noch tun? Stammfunktion der Parabel aufstellen:
f(x) = (-1/2)x² + (7/2)x - 3
F(x) = (-1/6)x³ + (7/4)x² - 3x + d
A = F(2) - F(1)
A = 13/12
Bei der Geraden könnten wir auch die Stammfunktion aufstellen und das Integral berechnen, ist aber nicht nötig, da wir es ja auch einfach als Flächeninhalt eines Dreiecks berechnen können.
g(x) = -x + 4
g(2) = -2 + 4
g(2) = 2
Wir haben also ein rechtwinkliges Dreieck mit einer Höhe und einer Länge von je 2 LE.
A = 2² / 2
A = 2
Das macht einen Flächeninhalt für die weiße Fläche von:
A = 13/12 + 2
A = 37/12
37/12 FE.
LG
Zunächst die Nullstellen von f(x) bestimmen. Davon wird nur die kleinere benötigt:
x1=1
Danach die Schnittstellen von f(x)=g(x) bestimmen. Davon wird ebenfalls nur die kleinere benötigt. Wir benennen sie
x2=2
Um die Fläche zwischen f(x) und der x-Achse zu berechnen, integrieren wir f(x) und erhalten das unbestimmte Integral
F(x)=-x^3/6+7x^2/4-3x+c
An der Stelle x1=1 soll die Fläche 0 sein. Also
F(1)=0=-1/6+7/4-3+c
Dies ergibt die Gleichung
c-17/12=0
mit der Lösung
c=17/12
Um die Fläche des Dreiecks zu bestimmen, setzen wir 2 in f(x) und erhalten für die senkrechte Dreiecksseite 2.
Für die waagrechte Dreiecksseite setzen wir g(x)=0 und erhalten 4. Davon 2 abziehen ergibt 2.
13/12+2×(4-2)/2=37/12
Und dies ist der Flächeninhalt der gesuchten weißen Fläche!