Wie berechne ich den Scheitelpunkt dieser Parabel?
Hallo meine Frage steht ja oben. Ich habe noch Schwierigkeiten den Scheitelpunkt abzulesen. Meine ganzen Klassenkameraden machen das In Sekunden schnell aber ich verstehe dass nicht. Kann mir das jemand an diesem Bild erklären wie ich den Scheitelpunkt heraus finden kann?:)
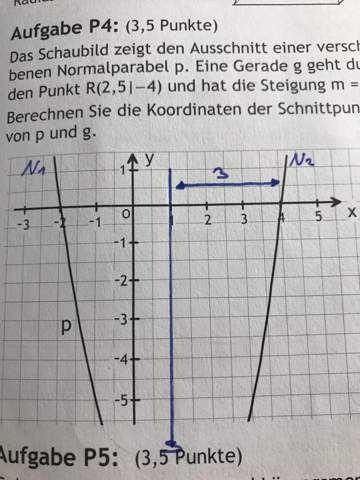
3 Antworten
es gibt für eine Parabel eine ganz grundlegende Fkt:
y = f(x) = a * (x - b)^2 + c
anhand von b und c kannst du hier den scheitelpunkt ablesen.
b wird auch x0 und c wird auch y0 genannt.
a ist die stauchung.
b und c sind die koordinaten des scheitelpunkts.
Da eine Parabel immer symmetrisch ist. Liegt der Scheitelpunkt immer gleich weit entfernt. So du hast die Nullstellen x1 =-2 und x2 =4 dann rechnest du einfach für die x- koodinte des Scheitels: (-2+4)/2 = 1 somit hast du die x - Koordinate und die y- Koordinate kannst du ja dann rauslesen. Allgemein für die x- Koordinate gilt: (x1+x2)/2
Der Scheitelpunkt einer Parabel liegt immer in der Mitte der beiden Nullstellen
Scheitelpunktform y=f(x)=a*(x-xs)²+ys
hier y=f(x)=1*(x-1)²+ys
a=1 weil eine Normalparabel,weder gestaucht noch gestreckt
Nullstelle bei x=4
f(4)=0=1*(4-1)²+ys=0=9+ys → ys=-9
y=f(x)=1*(x-1)²-9
binomische Formel (x-b)²=x²-2*b*x+b²
(x-1)²=x²-2*1*x+1²
f(x)=1*(x²-2*x+1)-9
f(x)=x²-2*x-8
Infos,vergrößern und/oder herunterladen

