Wert der Reihe berechnen?

Hat jemand einen Tipp wie man diese Reihe lösen kann? Komme seit Stunden nicht weiter und bekomme keinen vernünftigen Ansatz hin.

$\sum_{n=0}^{\infty}\frac{3+(-1)^k}{5^(k+1)}$

Eine Idee von mir ist, das Sandwich Lemma zu benutzen so das man die Folge

$a_{n\ }:=\ \frac{\left\{3+\left(-1\right)^k\right\}}{5^{^{\left(k+1\right)}}}\ ,\ b_n:=\ \frac{\left\{2\right\}}{5^{\left(k+1\right)}}\ ,\ c_{n\ }:=\ \frac{\left\{4\right\}}{5^{\left(k+1\right)}}$ nach

$b_n\le a_n\le c_n\ \$ abschätzen kann.

Allerdings weiß ich dann nicht, wie ich z.B den Wert der Reihe von

$\frac{\left[2\right]}{5^{\left(k+1\right)}}$ berechnen kann.

Würde mich sehr über Tipps freuen!

(Die Reihe scheint nach 1 zu konvergieren)

Answer 1

[mihisu]

Alternativ, anstatt die Reihe in zwei Reihen aufzuteilen:

Wenn man bereits weiß, dass die Reihe konvergiert (beispielsweise aufgrund des Majorantenkriteriums), also der Reihenwert existiert, kann man den Reihenwert in diesem Beispiel auch berechnen, indem man jeweils zwei aufeinanderfolgende Summanden (für geraden und ungeraden Summationsindex) zusammenfässt, um das (-1)^k in den Griff zu bekommen.

Comments

[DrunkenPigman]

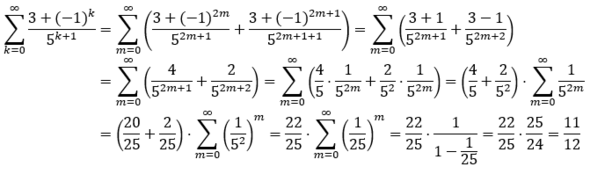
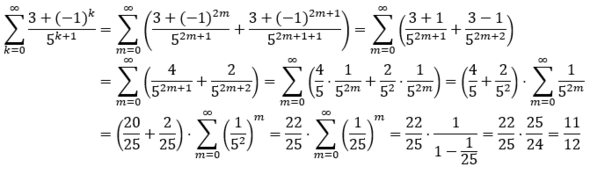
Okay das ist natürlich auch richtig praktisch, ich glaube diese Vorgehensweise kann ich ein einer anderen Aufgabe auch anwenden klasse Danke!!

Answer 2

[mihisu]

Erst einmal gehe ich davon aus, dass die Reihe

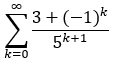
statt

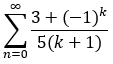
lauten sollte, warauf auch deine nachfolgenden Zeilen hindeuten.

Denn einerseits hast du sonst den Summationsindex n, aber bei deinen Summanden ein k stehen. Andererseits würde sonst, auch bei Verwendung von k als Summationsindex, die Reihe gegen unendlich divergieren.

============

Deine Abschätzung mit dem Sandwich-Lemma würde dir hier nicht den konkreten Reihenwert liefern, sondern nur, dass der Reihenwert zwischen 1/2 und 1 liegt.

Den Wert der Reihe

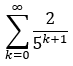
könnte man ermitteln, indem man die Reihe auf eine geometrische Reihe zurückführt. Und für geometrische Reihen sollte der Reihenwert bekannt sein:

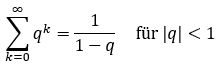
Demnach wäre also:

============

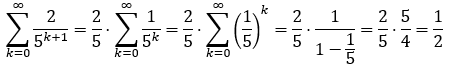
Bei der gestellten Aufgabe würde ich die Reihe in zwei Reihen aufteilen. Da die beiden Reihen

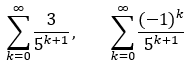
absolut konvergieren, ist:

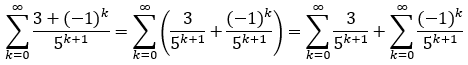
Führt man die einzelnen Reihen auf geometrische Reihen zurück, erhält man:

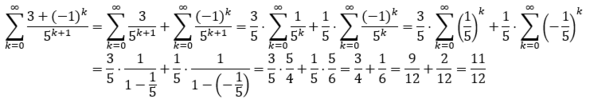
Der gesuchte Reihenwert ist demnach 11/12.

Comments

[DrunkenPigman]

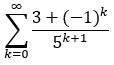
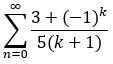
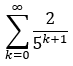
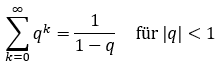
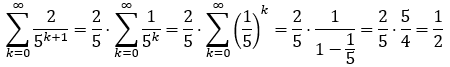
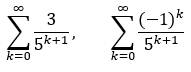
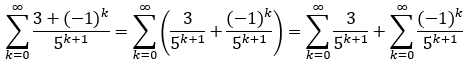
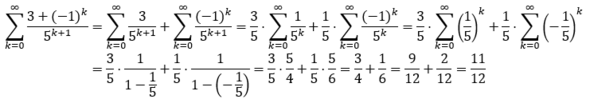
Super danke! Mit dem Wissen sind auch die anderen Reihen die ich noch lösen muss garnicht so schwer ;D Und da ich als Du mir erklärt hast wie man die geometrische Summenformel für die Abschätzung des Sandwich Lemmas benutzen kann, direkt das Wissen angewendet habe für das Auseinanderziehen der Summe (war auch ein fehlgeschlagener Versuch weil mir das Wissen fehlte) konnte ich diese selber lösen und bin aufs gleiche Ergebnis gekommen wie du ;D DANKEEEEE!!!! :D