Welche Dreiecke kann ich konstruieren?
Dass sind mögliche/unmögliche Dreieckskonstruktionen, wie kann ich OHNE konstruieren herausfinden ob diese Konstruktion möglich sind oder eben nicht?
VLG
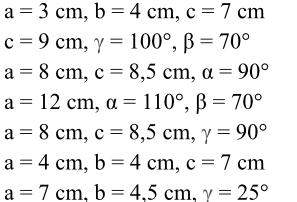
2 Antworten
a = 3 cm, b = 4 cm, c = 7cm
widerspricht der Dreiecksungleichung, denn jede Seite (hier c) muss kürzer als die Summe der anderen beiden Seiten (a + b) sein.
c = 9 cm, Gamma = 100°, Beta = 70°
Daraus folgt Alpha = 10°. Das ist machbar.
a = 8 cm, c = 8,5 cm, Alpha = 90°
Das ist ein rechtwinkliges Dreieck mit a als Hypotenuse. Wenn die Hypotenuse kürzer als eine Kathete sein soll, dann sieht das schlecht aus.
Alpha = 110°, Beta = 70°
Und wie groß soll dann Gamma sein?
a = 8 cm, c = 8,5 cm, Gamma = 90°
Diesmal ist c die Hypotenuse. Das bekommt man hin.
a = 4 cm, b = 4 cm, c = 7 cm
Das ist kein Problem.
a = 7 cm, b = 4,5 cm, Gamma = 25°
Auch das ist kein Problem.
widerspricht der Dreiecksungleichung, denn jede Seite (hier c) muss kürzer als die Summe der anderen beiden Seiten (a + b) sein.
Stimmt nicht. Die Dreiecksungleichung besagt c <= a + b.
mit c = a + b hat man ein "degeneriertes Dreieck" mit Fläche 0.
Folgende Beispiele, die nicht möglich sind.
Beispiel 1: a und b ergeben 7. Sind also gleichgroß wie c.
Dann wird das nichts mit einem Dreieck.
Beispiel 3: alpha ist ja 90°. Bildet somit eine Senkrechte auf Punkt A des Dreiecks.
Da a(8) kleiner als c(8,5) ist kann man auch kein Dreieck bilden.
Beispiel 4: 2 Winkel alpha und beta ergeben schon 180°.
Damit ist auch kein Dreieck möglich.