Warum erzeugen die Freiheitsgrade Vibration & Rotation eigentlich keine Erwärmung?
Temperatur ist eine thermodynamische Größe die alleine durch translation erzeugt wird.
Jetzt könnte man natürlich hinterfragen, wie dann eine Mikrowelle, die Energie in ein System pumpt welche dann anfangs als Rotation der Wassermoleküle gespeichert wird zu einer Temperaturerhöhung führt... das liegt daran, dass diese Energie schnell auf alle andere Freiheitsgrade verteilt wird - eben auch Translation (was bei Festkörpern eher ein wackeln um einen festen Punkt ist [jedoch nicht dasselbe wie der Vibrationsfreiheitsgrad]).
Nun Frage ich mich aber ganz allgemein, warum führt bloß Translation zu einer Erwärmung des Körpers? Rotation & Vibration sind doch ebenso Arten von Bewegungen und besitzen kinetische Energie - diese Bewegungen sind doch aller höchstens nicht ganz so umfangreich wie die Translationsbewegung aber deshalb tragen sie gar nicht zur Temperatur bei?? Klar, die dortige Energie wird immer wieder in Translation umverteilt etc., aber nehmen wir doch einfach für einen Moment an, dass es keine Translation gibt, nur Rotation und Vibration.
Warum müssen sich Molekül als ganzes (Translation ) für Erwärmung bewegen?
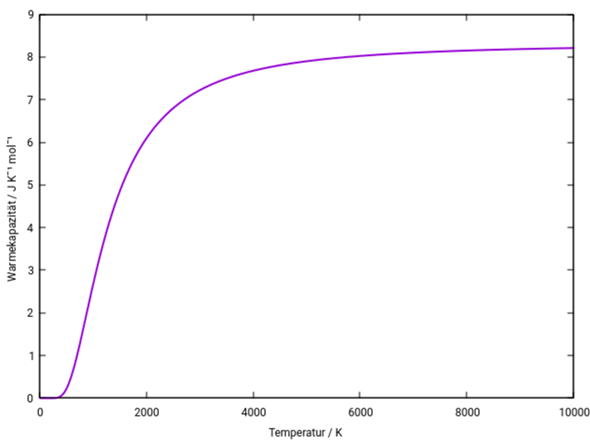
Man sieht auch anhand dieses Diagramms, dass die Wärmekapazität erst mit Rotation und Vibration steigt, eben weil die dortige gespeicherte Energie nicht zur Temperaturerhöhung führt und entsprechend mehr Energie rein muss um T weiter zu erhöhen:
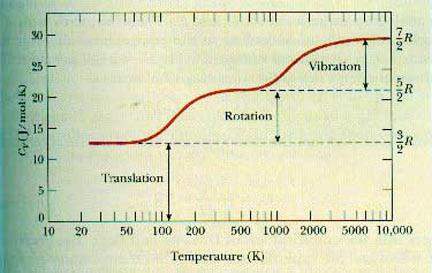
Ich möchte nochmal betonen, dass natürlich durch die Natur der Gleichverteilung letztendlich jeder (Translation, vibration, Rotation) Freiheitsgrad ½kT hergibt und Temperatur über diese Denkweise durch alle 3 gemessen werden kann (denn so betrachtet macht es keinen Unterschied welchen Freiheitsgrad man betrachtet, alle 3 tragen gleich viel bei), doch ich habe als Gedankenexperiment trotzdem Translation ausgeschlossen.
Mir ist schon aufgefallen, dass man bei dieser Frage sehr bedachte Worte wählen muss, beispielsweise lässt sich über die Aussage streiten:
Rotation und Vibration beeinflussen nicht die Temperatur.
Manche führen als Gegenbeispiel an, dass wenn man kurz das System anhält, alle Rotationsenergien rausnimmt und es dann wieder laufen lässt, die Temperatur gefallen sein muss und somit Rotation die Temperatur beeinflusst. JA, aber bloß weil durch die zusammenstöße diese weggefallenden Zustände wieder teilweise "aufgefüllt" wurden und sich somit die Translationsenergie natürlich ebenfalls verringert hat... für mich ist das keine direkte Beeinflussung der Temperatur, sondern das Resultat der Gleichverteilung das indirekt dazu führt, dass die Translationsenergie geringer wird und darum die Temperatur sinkt.
2 Antworten
Die vorhandene thermische Energie ist zwischen allen Freiheitsgraden verteilt. Wenn Du einen Freiheitsgrad spezifisch mit Energie fütterst, dann gibt er diese Energie sehr rasch an die hungrigen Kollegen weiter (dazu kann es Ausnahmen geben), weil die Moleküle dauernd aneinander stoßen und dabei Energie austauschen. Direkte Kopplungen zwischen den Freiheitsgraden existieren im Fall von Schwingungen, die können auch ohne Stoße untereinander Energie hin- und hertransferieren (das funktioniert über Anharmonizitäten: Wären die Schwingungen rein harmonisch, dann ginge es wirklich nicht).
Der Energieaustausch beim Stoß erfolgt unkontrolliert, unspezifisch und in jede Richtung. Weil es aber viele Teilchen sind, ergeben sich zwangsläufig statistische Regelmäßigkeiten. Im Mittel enthält jeder Freiheitsgrad eines Moleküls bei einer bestimmten Temperatur eine bestimmte Energie — bei Translation und Rotation ist das ½RT, bei Schwingungen ist das komplizierter. Für rein harmonische Schwingungen erhält man eine geschlossene Formel mit der Anregungsenergie ε₀ und einer hyperbolischen Winkelfunktion:
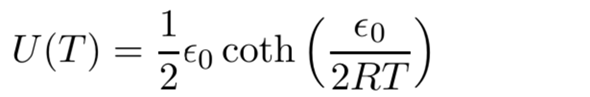
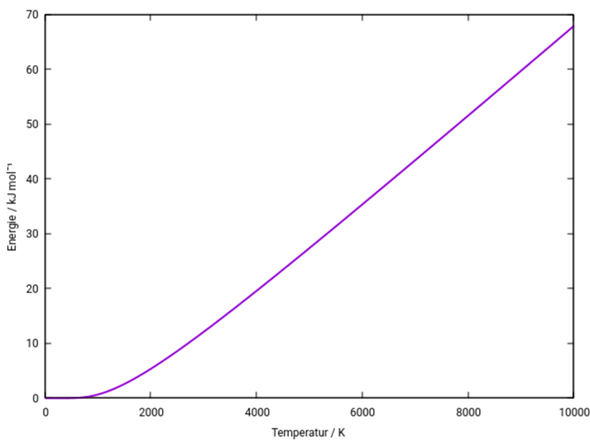
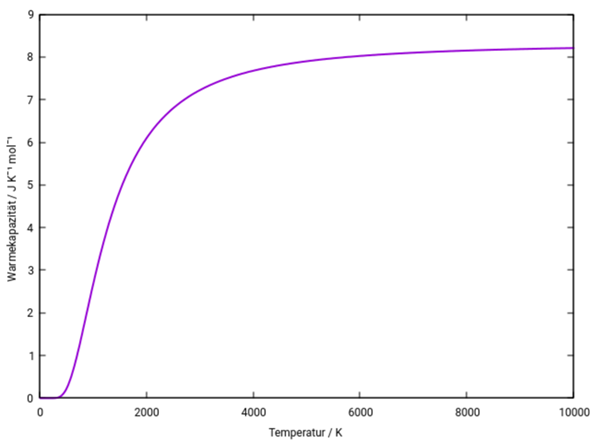
und man kann solche Formeln auch näherungsweise für anharmonischen Modellpotentiale ableiten (ich weiß das aus erster Hand, weil ich solche Sachen in meiner Dissertation gemacht habe). Harmonische Schwingungen nehmen übrigens bei tiefen Temperaturen T≪ε₀/R nur sehr wenig Energie auf, bei hohen T≫ε₀/R dagegen doppelt soviel wie Rotation und Translation; das siehst Du, wenn Du die Funktion U(T) für irgendein Beispielmolekül, z.B. N₂ mit ε₀=33 kJ/mol, plottest (die Nullpunktsenergie ist in der Formel enthalten, aber ich habe sie aus dem Plot rausgerechnet, weil ich es so für übersichtlicher halte).
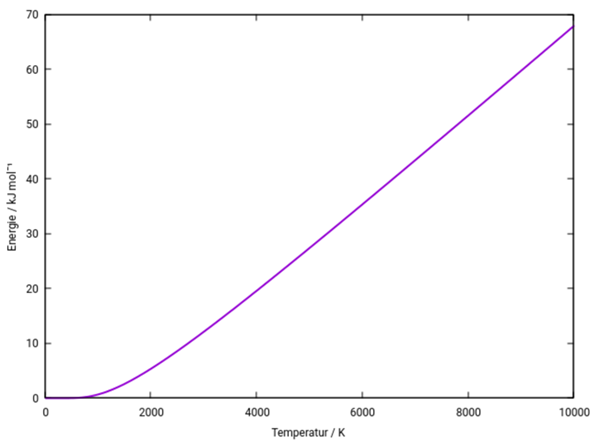
Du siehst, daß die Schwingung des N₂-Moleküls bei tiefen Temperaturen, z.B. Raumtemperatur, wirklich keine Energie aufnehmen kann, aber oberhalb von ε₀/R≈4000 K siehst Du einen linearen Anstieg mit Steigung R.
Im allgemeinen reden also alle Freiheitsgrade mit, wenn es darum geht, eine vorhandene Menge Energie in eine Temperatur zu übersetzen, oder umgekehrt halten sie bei einer gegebenen Temperatur alle einen Anteil an der Gesamtenergie. Warum Du das Gegenteil behauptest, weiß ich nicht (oder ich habe Dich mißverstanden).
Wahr ist allerdings, daß man die Temperatur nur aus der Teilchengeschwindigkeit, also der Energie im Translationsfreiheitsgrad, bestimmen kann — wenn Du weißt, wie schnell die Teilchen in eine bestimmte Richtung fliegen, dann gilt E=½mv²=½RT, und Du kannst die Geschwindigkeit auf Temperatur umrechnen. Dasselbe könntest Du aber ebensogut mit einem Rotationsfreiheitsgrad machen (Du bestimmst die Rotationsgeschwindigkeit, und E=½Iω²=½RT wie oben). Theoretisch könntest Du das auch mit Schwingungen machen, aber wegen der komplizierten Umrechnung zwischen Temperatur und Energie pro Freiheitsgrad ist das weniger praktisch. Trotzdem kann man manchmal Eigenschaften bestimmter Schwingungen aus temperaturabhängigen Meßgrößen bestimmen, z.B. die Tiefe von Potentialtöpfen aus der NMR-Koaleszenztemperatur.
P.S.: Hier ist die Wärmekapazität der Schwingung im N₂, erhalten als Ableitung der Energie oben nach der Temperatur.
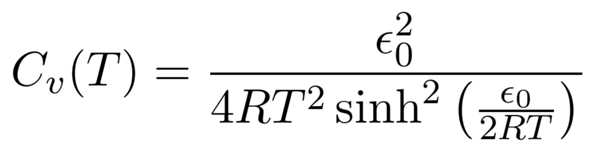
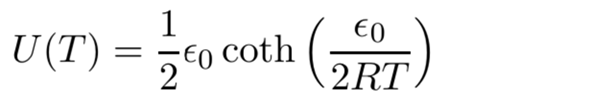
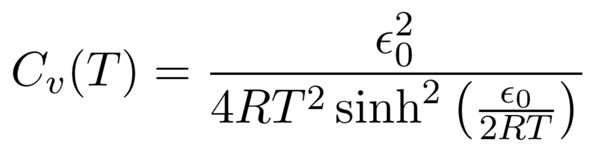
Das ist jetzt wieder so ein Beitrag, wo ich als Praktiker staunend daneben stehe. ;)
Im allgemeinen reden also alle Freiheitsgrade mit, wenn es darum geht, eine vorhandene Menge Energie in eine Temperatur zu übersetzen, oder umgekehrt halten sie bei einer gegebenen Temperatur alle einen Anteil an der Gesamtenergie. Warum Du das Gegenteil behauptest, weiß ich nicht (oder ich habe Dich mißverstanden).
Verschiedene Quellen betonen immer wieder, dass nur die lineare Bewegung von Molekülen (Translation) die Temperatur bestimmt.
Beispiel:
We also pointed out that temperature is a measure of the average kinetic energy due to translational motions of molecules. If vibrational or rotational motions are also active, these will also accept thermal energy and reduce the amount that goes into translational motions. Because the temperature depends only on the latter, the effect of the other kinds of motions will be to reduce the dependence of the internal energy on the temperature, thus raising the heat capacity of a substance.
Ich glaube, Du sitzt einem sprachlichen Problem auf.
Ich habe ja geschrieben, daß die Temperatur eindeutig nur aus einem einzigen Freiheitsgrad bestimmt werden kann, am einfachsten aus der Translation. Jeder Freiheitsgrad enthält bei einer gegebenen Temperatur eine bestimmte Menge Energie, und wenn man die mißt, dann weiß man die Temperatur.
Wenn Du z.B. mißt, daß die Schwingung im N₂ 30 kJ/mol thermische Energie enthält (indem Du z.B. bestimmst, wieviele Moleküle in den einzelnen Schwingungsniveaux sitzen und dann mittelst), dann kannst Du mit der Graphik oben verifizieren, daß die Temperatur T=5337 K sein muß. Manche würden vielleicht deshalb sagen, daß die Temperatur nur von der Schwingungsenergie abhängt, aber ich halte das für eine Krumme Formulierung™, weil das ja für jeden Freiheitsgrad gilt.
Und in Deinem Zitat wird ja auch korrekt gesagt, daß ein Teil der thermischen Energie in die anderen Freiheitsgrade fließt.
Das ist wahrscheinlich eine Kombination aus sprachlichen Problem und irgendetwas unbekannten. Machen wir es mal so: Nehmen wir Mal das fiktive Beispiel an, es gäbe keine Translation und die gesamte Energie könnte sich nur auf Rotation, Vibration (und Elektronische Anregungszustände [wobei das nach der Partitionsfunktion bei humanen Temperaturen kaum beiträgt]) verteilen. Wir pumpen nun immer mehr Energie rein und halten unsere Hand auf den Körper, würden wir uns irgendwann verbrennen weil die Temperatur steigt?
Dein „fiktives Beispiel“ ist bei jedem Festkörper erfüllt, weil es da nur Schwingungen, aber keine Translation (und meist auch keine Rotation) gibt. Können Festkörper heiß sein? Natürlich, weil Energie aus ihren Schwingungsfreiheitsgraden in Deinen Körper abfließt und dort Ärger macht.
In einem Festkörper gibt es weiterhin Translation, sie ist zwar gehindert: Sie bewegt sich nicht in einer geraden Linie üner eine nennenswerte Strecke, aber es handelt sich dennoch um eine Translation. Die Bewegung in einem Festkörper ist dann eben ähnlich einer Schwingung. Diese Schwingungstranslation ist dann natürlich nicht mehr vollständig von molekülschwingungen etc. als Translationsbewegung der molekularen Massenzentren zu trennen.
Wenn sich der Schwerpunkt im Mittel nicht bewegt (also kein Impuls auftritt), dann ist es keine Translation. In einem normalen, gut gebundenen Festkörper kommt kein Atom weit von seinem Gitterplatz weg (kann nur um ihn herumeiern), und der Schwerpunkt legt keine Strecke zurück. Das liegt daran, daß der Gitterplatz das Minimum eines Potentials ist, zu dessen Überwindung die thermische Energie bei weitem nicht reicht.
Wenn Du das anders siehst, dann müßtest Du auch Molekülschwingungen „irgendwie“ oder „teilweise“ als Translationen sehen, denn die Atome bewegen sich ja kurzfristig, bevor sie wieder wieder zum Minimum des Potentialtopfes zurückgezogen werden.
Das ergibt Sinn. Ok dann tragen also sowohl Vibration als auch Rotation zur Temperaturerscheinung bei. Was ist mit Elektronischer Energie, also angeregte zustände? Die werden (ich nehme jetzt nur die ersten 2 relevanten Terme) durch die Partitionsfunktion q_elec(T)= g1 + g2 * exp(-e2/[kT]) + ... beschrieben. Trägt dieser Freiheitsgrad ebenfalls zur Temperatur bei wenn bei hohen Temperaturen langsam diese Zustände besetzt werden? Und wenn du sagst das Rot. & Vib. zur Temperatur in unserem kommunizierten Verständnis beiträgt, wie kommt es dann bei zunehmender Besetzung deren zustände zu einer Erhöhung der Wärmekapazität? Würden sie nicht zur Temperatur beitragen würde das ja noch irgendwie Sinn ergeben, dann würde immer mehr Energie in diese Zustände fließen und diese würde nicht zur Temperatur beitragen, was natürlich C wachsen lässt.
Sorry ich will dich nicht nerven, nur ein wenig Klarheit in meinem Kopf schaffen 😅
Die Wärmekapazität von Rotationsfreiheitsgraden ist (außer bei sehr niedrigen Temperaturen) konstant ½R pro Freiheitsgrad. Bei der Schwingung ist es komplizierter; ich habe in der Antwort eine entsprechende Graphik fürs N₂-Beispiel nachgetragen.
Ein System, das nur elektronische aber keine mechanischen Freiheitsgrade hat, kann ich mir nicht vorstellen (es muß ja wohl alles aus Atomen bestehen, oder?). Aber unter der Voraussetzung, daß diese Elektronen einen effizienten Mechanismus haben, mit meinem Körper Energie auszutauschen, werden sie sich auch heiß anfühlen. Denn alle Freiheitsgrade wollen (und bekommen nach statistischen Gesetzmäßigkeiten) einen Anteil an der Energie, und das trifft leider auch für die Freiheitsgrade in meinem Gewebe zu.
(Es gibt magnetische Spin-Systeme, die zwar auch eine Temperatur haben aber kaum mit nichtmagnetischer Materie wechselwirken. Mangels eines Energieübertragungsmechanismus können sie sich kalt anfühlen, obwohl sie vielleicht Tausende K heiß sind. Man sagt, diese magnetischen Freiheitsgrade sind von den anderen entkoppelt. Daher ist es sogar möglich, Systeme herzustellen, die „zwei Temperaturen gleichzeitig“ haben, eine Temperatur der Kernspins und eine konventionelle. Kernspins lassen sich in einem Magnetfeld mit Radiowellen auf fast beliebig hohe Temperatur aufheizen. Das ist aber nur ein temporärer Effekt, weil das System nicht im Gleichgewicht ist; wartet man lange genug, dann stellt sich natürlich thermisches Gleichgewicht ein, und jeder Freiheitsgrad hat das, was ihm laut Temperatur zusteht).
Puh, es gibt so viele Informationen die was anderes behaupten, ich dachte das ich wenigstens etwas bescheid wüsste aber sobald ich nachbohre merke ich wieder, dass ich so gut wie nichts weiss 😅 obwohl ich statistische Thermodynamik, Physik 1&2, Experimentalphysik Praktikum und Physikalische Chemie 1 gut bestanden habe...
Da denke ich mir nur, vielleicht sollte ich dieses brisante vordringen etwas zurückfahren und die nächsten Jahre bis ich ca. 26-30 Jahre alt bin nur von anderen (Professoren, Lehrbücher) lernen bis ich anfange solche Fragen zu stellen.
Ich habe das alles auch erst verstanden, als ich mir an der theoretischen Physik eine Vorlesung Statistische Physik reingezogen habe. Peinlicherweise war das erst parallel zu meiner Dissertation (ich bin Chemiker).
Das ist irgendwie beruhigend zu hören :-) Habe das auch von anderen so ähnlich mitbekommen, bin gerade in meinem Chemie Bachelor.
Es ist einfach schwer zu akzeptieren das dass angebliche Wissen nichts als Illusion ist, es ist höchstens praktischer Erfahrungswert.
Ich glaube je länger man mit diesen Themen einfach nur in Kontakt steht, desto besser wird es. Auch Themen von denen man denkt, man hätte sie verstanden, sollte man wohl auch immer wieder so aufnehmen, als würde man sie zum aller ersten Mal hören (total unvoreingenommen).
Kleinkinder haben im Vergleich zu uns ja auch eine viel höhere Lernkapazität, weil es noch nicht so viele verfestigte Denkmuster gibt und auch noch kein richtiges "Ziel Denken".
Oft stehen mir solche Fragen - wie diese zum Beispiel - im Weg, weil ich in der Zeit dann nichts anderes machen kann. Dieses verharrene Wissen wollen erreicht paradoxerweise genau das Gegenteil. Ähnliche Muster bemerke ich auch beim meditieren, sobald man zu sehr versucht irgendetwas erreichen zu wollen bewirkt dass genau das Gegenteilige. Die ganze Kunst des Lebens liegt im Grunde in einer feinen Balance zwischen Loslassen und Festhalten....
Vielleicht ist eine vorsichtige mikroskopische Definition der Temperatur folgende?
Temperatur ist die mittlere Energie, die in den verfügbaren Zuständen/ Freiheitsgraden/ mikrozuständen des Systems gespeichert ist.
Das inkludiert nun auch alle möglichen Zustände der Boltzmann Statistik:
Elektronisch >> Vibration > Rotation >> Translation.
Meine Definition schließt nun nicht nur kinetische vib., rot. und tra. ein, sondern eben auch die kinetische und potentielle Energie des Elektrons bei Anregungen in energetisch höhere Orbitale. Jetzt habe ich bewusst das "mittlere kinetische Energie der Translation" ausgelassen, theoretisch betrachtet ist diese Definition natürlich absolut gleichwertig.
Man hätte auch schreiben können "ist die mittlere Energie der Vibration" oder die mittlere Energie über alle Einzelzustände der elektronischen Energie... ist am Ende alles gleich.
Oder wir definieren Temperatur nur anhand von Potentiellen Energien, falls sie auftauchen. Sobald Energie irgendwo als potentielle Energie gespeichert wird (Wechselwirkung zwischen Translation), Vibration, ja sogar Rotation bei Wechselwirkungen sollte nach dem Gleichverteilungssatz auch darauf gleichermaßen umgelagert werden und wir könnten sagen:
Temperatur ist der Mittelwert der Potentiellen Energien aller Mikrozustände in denen Potentielle Energie gespeichert werden kann.
Oder man betrachtet einfach den Durchschnitt von Kinetischer + Potentieller zusammen.
Diese erweiterten Definitionen sind im Gleichgewicht natürlich alle absolut gleichwertig aber vielleicht ist die eine oder andere Definition im nicht thermodynamischen Gleichgewichtsfall praktischer um etwas zu untersuchen?
Was ich in deinen Ausführungen vermisse ist die Unterscheidung zwischen den Aggregatszuständen, denn die haben auf obige Argumentation einen entscheidenden Einfluss.
In einem idealen Gas, in dem sich die Teilchen extrem schnell über große Entfernun gen bewegen, ist die Temperatur (praktisch) nur von der kinetischen Energie der Translation abhängig. Rotation und Eigenschwingung sind im Vergleich dazu vernachlässigbar.
In einem Metallkristall (Fetskörper) sieht es dagegen ganz anders aus. Da spielt die kinetische Energie einer translatorischen Bewegung überhaupt keine Rolle. Die Teichen stecken im Kristallgitter fest und können sich nicht bewegen. Allenfalls die Elektronen bewegen sich translatorisch, aber die haben kaum Masse und kaum Geschwindigkeit, sodass das keine Rolle spielt. Im Kristallgitter eines Metalls steckt die thermische Energie in den Schwingungen der Teichen sowie in der potentiellen Energie. Die einzelnen Teilchen befinden sich gegenseitig in ihren Kraftfeldern. Mit der Erwärmung des Kristalls nimmt die Entfernung der Teiklchen zueinander zu, die potenzielle Energie steigt. Das merkt man phänomenologisch auf der Makroebene durch die Wärmeausdehnung.
Oder: https://youtu.be/nqGtji3ZjoI?si=q_Pou0jjTo0Yps1C
Am Anfang, Aussage ab 00:38 :
Es ist nur die Bewegung der Moleküle durch den Raum und nicht ihre Rotation, die zur Temperatur beiträgt.