Wärmekapazität Wasser?
Die Frage lautet:
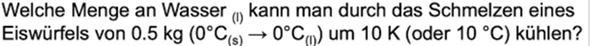
Die Wärmekapazität von Eis ist offenbar 2060 J/kg * °C.
Ich bin bisher so vorgegangen:
Wärmekapazität Wasser (s) cw = 2060 J / kg * °C 0,5kg = 1030 J
Q / DT * cw = mw
Q / -10 °C * 1030 J = mw
Aber nun habe ich ja zwei Unbekannte ...?
2 Antworten
Aufgenommene Schmelzwärme Qs:
Qs = q * m = 0,5 kg * 334 kJ/kg = 167 kJ
Dieselbe Wärme wird dem Wasser entzogen:
Q = m * c * ∆T
m = Q / (c * ∆T) = 167 kJ / (4,2 kJ/kgK * 10 K) = 3,977 kg
Danke vielmals. Das klingt einleuchtend. Aber wie kommst du auf 4,2 kJ/kgK?
4,2 kJ/kgK ist gerundet und weicht weniger als 1 % vom minmalen Wert 4,18 bei 40 °C und dem maximalen Wert von 4,22 bei 0°C ab. Wenns nicht genau aufs Gramm drauf ankommt kann man immer mit 4,2 über den gesamten Temperaturbereich rechnen.
Die Wärmekapazität von Eis ist offenbar 2060 J/(kg*K) .
Ich ergänze: Das gilt für 0 °C und stimmt.
Wärmekapazität Wasser (s) c w = 2060 J / kg * °C 0,5kg = 1030 J
Keine Ahnung was du da rechnest und warum überhaupt. Denn die Wärmekapazität für Wasser bei 0 °C ist ein Literaturwert der da lautet 4220 J/(kg*K).
Und dann darf man natürlich die Schmelzenthalpie nicht vergessen.
Konnte ich dir so auf die Sprünge helfen?
Noch ein Tipp: Die Wärmekapazität vom Eis ist nicht relevant für die Berechnung.
Ich hab's glaub verstanden. 4,2 kJ ist einfach die Wärmekapazität von Wasser (allerdings bei 25 C, wenn's mir recht ist). Danke für die super Erklärung!