Waagerechte Tangente auf Graphen bestimmen?

Wie kann man die Aufgabe 4 lösen?
Benötige es für die morgige Klausur.
2 Antworten
fa(x) = (-x^2 + a)*e^-x
Für Tangenten brauchen wir die 1. Ableitung:
fa'(x) = (x^2 -2x - a)* e^-x
Waagrechte Tangente, also:
(x^2 -2x - a)* e^-x = 0
Satz vom Nullprodukt: Ein Produkt ist dann = 0, wenn einer der Faktoren = 0 ist.
Da e^-x niemals 0 wird, muss also gelten:
x^2 -2x - a = 0
Das lösen wir mit der pq-Formel. Die hat dann genau eine Lösung, wenn der Ausdruck unter der Wurzel = 0 ist. Daher
(p/2)^2 - q = 0
mit
p = -2
q = -a
(-1)^2 + a = 0
a = -1
Damit lautet die gesuchte Funktion:
f_-1(x) = (-x^2 - 1)*e^-x
Zusatz:
aus:
x^2 -2x + 1 = 0
ergibt sich alleine durch hingucken:
x = 1
Also liegt die Waagrechte Tangente bei x = 1
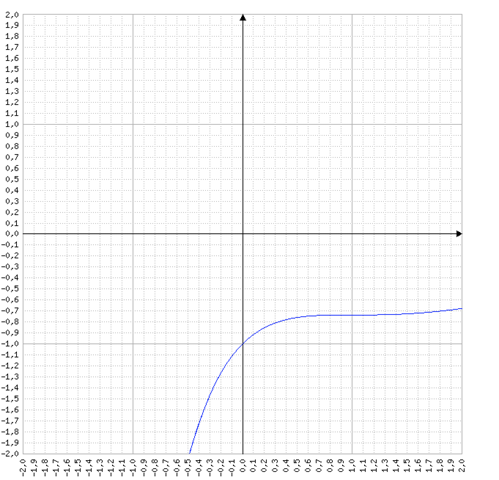
Und so sieht das als Graph aus:

..offensichtlich handelt es sich hier um einen Sattelpunkt (Wendepunkt mit waagrechter Tangente).
Leite f_a(x) ab und berechne die Nullstellen der Ableitung in Abhängigkeitvon a. Bestimme a so dass nur eine (doppelte) Nullstelle existiert.