Unterschied bei ebenengleichung?
Was ist der Unterschied von einer Parameterform einer Ebene und von dieser Gleichung wo man nach x1 x 2 x3 Auflösen muss..warum gibt es bei der parameter form einen Ortsvektor wo die Ebene dann anfängt und bei der Gleichung muss man von den Schnittstellen auf der koordinatenachsen anfangen..Was ist der unterscheid?Ist es nicht das selbe nur anders geschrieben?Warum gibt es bei der Gleichung keinen Ortsvektor wo die Ebene bei der selben Stelle anfängt ?
Zb hier wo man von den Achsen anfängt:
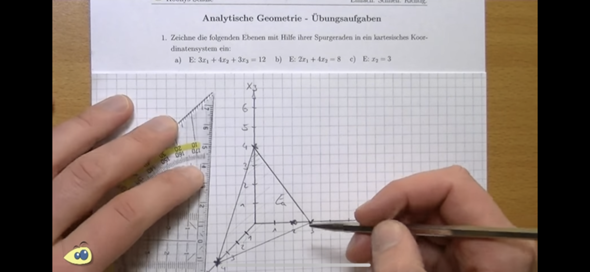
2 Antworten
Was ist der Unterschied von einer Parameterform einer Ebene und von dieser Gleichung wo man nach x1 x 2 x3 Auflösen muss
Bei der Parameterform wird die Ebene durch einen Stützvektor und zwei Richtungvektoren Beschrieben. Bei der Koordinatenform wird die Ebene als Lösung einer Linearen Gleichung beschrieben.
warum gibt es bei der parameter form einen Ortsvektor wo die Ebene dann anfängt und bei der Gleichung muss man von den Schnittstellen auf der koordinatenachsen anfangen
Der Ortsvektor bzw die Schnittstellen mit den Koordinatenachsen dienen nur dazu, um die Ebene leichter graphisch darzustellen. (Bei der Koordinatenform kann man die Schnittstellen sehr einfach ablesen)
Was ist der unterscheid?Ist es nicht das selbe nur anders geschrieben?
Genau das sind einfach nur 2 unterschiedliche Schreibweisen um Ebenen festzulegen. Jede Ebene kann man durch beide Darstellungsarten Darstellen.
Warum gibt es bei der Gleichung keinen Ortsvektor wo die Ebene bei der selben Stelle anfängt ?
Weil sowas nicht benötigt wird, da die Ebene durch die Gleichung sofort eindeutig bestimmt ist. Und wie gesagt, eine Ebene hat keinen Anfangspunkt.
Die verlaufen nicht anders. Wenn die Ebene eine Achse nicht schneidet, dann kommt die Koordinaten in der Gleichung nicht vor.
x1=1 beschreibt z.b die Ebene die Parallel zur x2-x3 Ebene ist, und durch den Punkt (1, 0 ,0) geht.
Hattet ihr denn schon die Nornalenform?
Der unterschied ist die Notation, nicht mehr und nicht weniger
Also wäre beides das selbe?Warum verläuft das dann anders bzw. Fängt von wo anders an?
Und wieso verläuft die Ebene der Parameterform anders?Bei der Koordinatenform werden die Achsen geschnitten und bei der parameterform nicht immer ..