Titration von Essigsäure mit Natronlauge - Aufgabe?
Hallo,
hab eine Aufgabe welche ich "gelöst" hab, jedoch mir unsicher bin ob diese richtig sein kann.
Skizzieren Sie die Titrationskurve für eine 0.1 M Essigsäure-Lösung mit einer 0.5 M Natronlauge. Berechnen Sie hierfür die pH-Werte bei der Zugabe von Äquivalenten für T=0, 0.5, 1, 2. (Unter der vereinfachten Annahme, dass die Volumenzunahme durch die Basenzugabe ignoriert werden kann).
Bei T=0, besteht die Lösung nur aus Essigsäure, welche mit einem pKs=4.8 eine schwache Säure und damit pH=0.5(4.8-lg(0.1))=2.9.
Bei T=0.5, neutralisiert sich die Hälfte von Essigsäure durch die starke Base NaOH, damit pH=0.5(4.8-lg(0.05))=3.05
Bei T=1, vollständige Neutralisation von HAc und NaOH, aber da HAc eine schwache Säure, Rückblieb von 0.1 M Ac-, mit pkB= 9.24. Damit gilt pOH=0.5*(9.24-lg(0.1))=5.12 und damit ph=14-5.12=8.88.
Bei T=2, gleich wie bei T=1 nur 0.1 NaOH, mit pkB=-0.56. Die stärkere Base verdrängt die schwächere Base (warum?) und damit gilt 14-0.6*(-0.56-lg(0.1))=13.78
Ist das Richtig?
1 Antwort
Dein Ansatz ist nicht ganz sauber. Denn bei T=½ hast Du ja die Hälfte der Essigsäure zu Acetat neutralisiert und die andere Hälfte ist noch da. Deshalb liegt ein symmetrischer Puffer vor (Acetat=Essigsäure), und pH=pKₐ=4.75
Bei T=2 hast Du richtig erkannt, daß eine NaOH-Lösung vorliegt, also eine starke Base, deren pH Du einfach ausrechnest als pH=14+lg(c). Es bleibt nur noch, die Konzentration zu bestimmen. Wenn Du (wie in Deiner Angabe verlangt) die Volumszunahme durch die Basenzugabe vernachässigst, dann ist c=0.1 mol/l (pH=13), real c=0.071bzw. pH=12.85. Was Du gerechnet hast, kann ich nicht nachvollziehen.
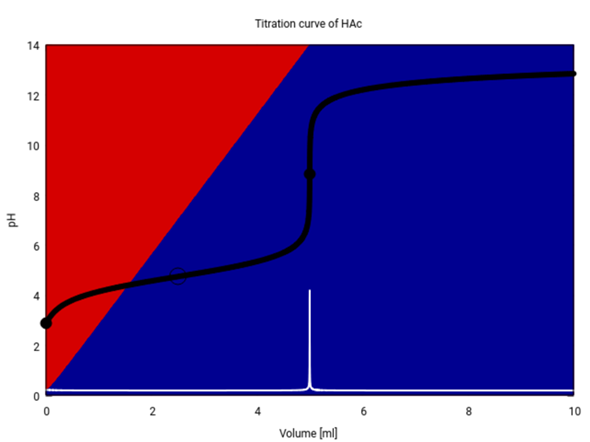
Ich zeige Dir hier, wie die Titrationskurve wirklich aussieht: 25 ml 0.1 mol/l Essigsäure titriert mit 0.5 mol/l NaOH. Der Äquivalenzpunkt (T=1) liegt bei 5 ml.
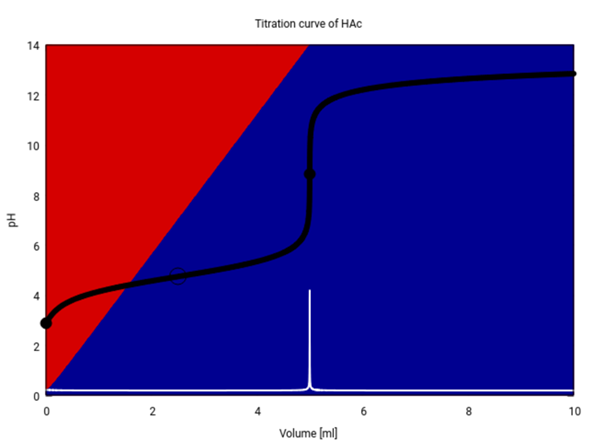
Die Titrationskurve ist schwarz und ihre erste Ableitung weiß eingezeichnet. Die Hintergrundfarben verraten, wieviel CH₃COOH (rot) bzw. CH₃CO₂⁻ (blau) in der Lösung real vorliegen. Bei T=½ (2.5 ml, Hohlkreis) ist es genau 1:1.