Tipps zur Wahrscheinlichkeitsrechnung?
Hallo,
ich lerne derzeit für die Wahrscheinlichkeitsrechnung und eigentlich habe ich die Grundlagen auch alle verstanden und kann sie anwenden.
Probleme habe ich jedoch bei Aufgaben, bei denen man die Ergebnisse mehrerer Pfade eines Baumdiagrammes zusammenrechnen muss, wenn ich diese Aufgaben lösen möchte, ohne ein solches Baumdiagramm zu zeichnen. (Denn das braucht ja auch immer einiges an Zeit...) Also: kurz gesagt: ich habe Probleme damit zu bestimmen, wie viele Pfade die ich addieren muss, vorhanden sind...
Ich weiß zwar, dass es da die Bernoulli-Formel gibt, jedoch klappt diese auch nicht immer und ehrlich gesagt habe ich diese auch noch nicht ganz perfekt drauf... :/
Deshalb meine Frage: Gibt es da irgendeinen Trick, den man da zuverlässig anwenden kann?
Denn im Internet finde ich da auch nichts und gerade in Mathe stehe ich total darauf, Tricks zu finden, die immer klappen und die dadurch Sicherheit geben, wenn man z.B. eine Klausur über ein bestimmtes Thema schreibt... :D
Ich hoffe, dass irgendjemand dem folgen konnte und für eine Antwort die mir da helfen würde, wäre ich unglaublich dankbar!!!!!
Wenn möglich werde ich auch die beste Antwort aussuchen... :)
3 Antworten
Da du von Pfaden addieren redest, würde ich gerne fragen... bist du mit den Pfadregeln vertraut?
Kannst du eine Beispielsaufgabe nennen, damit ich mir ein besseres Bild verschaffen kann?
Man hat 3 Würfel, welche alle gleichzeitig 3x hintereinander geworfen werden.
Wie groß ist die Wahrscheinlichkeit dafür, dass insgesamt nur 1x die Zahl 4 erscheint?
Diese Aufgabe habe ich mir gerade spontan ausgedacht, weil ich nicht weiß, ob es eventuell Urheberrechtsprobleme geben könnte, wenn ich eine Aufgabe aus meinen Büchern nehme. ;)
Deshalb habe ich jedoch keine Lösung parat. ;)
Und nochmal vielen,vielen Dank dafür, dass Du dich so bemühst, mir zu helfen!!!! :)
Um schrittweise heranzugehen: Wenn man 3 Würfel gleichzeitig wirft...
...die Wkt, keine 4 zu würfeln, ist 5/6 * 5/6 * 5/6 = 125/216
...die Wkt, genau eine 4 zu würfeln, ist 1/6 * 5/6 * 5/6 * 3 = 75/216 (mal 3 deshalb, weil es ja drei Mkts für einen Würfel gibt, der die 4 anzeigt)
... die Wkt, zwei oder mehrere Male die 4 zu würfeln, ist die Wkt des Gegenereignisses: 1 - 125/216 - 75/216 = 16/216
Kannst du mir soweit folgen?
Und jetzt würde ich ein Bumdiagramm zeichnen - hab ich nochmal in einer neuen Antwort geschickt.
Nun muss man eigentlich nur noch die Pfadregeln anwenden, um auf die Lösung zu kommen.
Wenn du willst, dass genau einmal eine 4 gewürfelt wird, brauchst du einen Pfad mit zweimal rot und einmal grün.
Die Wkt für einen solchen Pfad beträgt: (125/216) * (125/216) * (75/216) = 0,116 (gerundet)
(nach 1. Pfadregel)
Im Baumdiagramm gibt es drei dieser entsprechenden Pfade. Deshalb ist die Wkt für das von dir angefragte Ereignis:
0,116 + 0,116 + 0,116 = 0,348
(nach 2. Pfadregel)
"Nur teilweise gibt es ja auch Aufgaben, bei denen man noch mehrere Ergebnisse dieser Mulitplikationen addieren muss"
Das
ist genau das, was wir hier gemacht haben. Es beschreibt die 2.
Pfadregel. Auf der olgenden Seite wird das nochmal schön erläutert:
Der Bernoulliversuch kennt nur T=Treffer und N=Niete.
Formel P(ges)= (n7k) * p^k * (1-p)^(n-k)
mit (n/k)= n!/(k! * (n-k)! ist der Binominalkoefizient.Dieser gibt an,wie viel Pfade bei den Bedingungen existieren.
Beispiel : Ein Würfel wird n=6 mal geworfen.Wie hoch ist die Wahrscheinlichkeit ,das die 3 K=2 mal kommt ?
Wahrscheinlichkeit für die 2 ist P(2)=1/6=0,166 =16,66 %
Dies ist das p=0,166 in der Formel .Werte eingesetzt
P(ges)= 6!/2! * (6-29! * 0,166^2 * (1-0,166)^(6-2)=0,199=19,9 %
Beispiel : Die 3 soll am Ende des Versuchs kommen,beim letzten Wurf
Hier gibt es nur 1 Pfad und zwar
Pfad N-N-N-N-N-T
Wahrscheinlichkeit für eine Niete P(N)=1-0,166=0,8334
eingesetzt P(ges)= 0,8334^5 *0,166=0,0667= 6,67%
"Kombinatorische Abzählverfahren"
Produktformel : n1*n2*n3* nk = Anzahl der möglichen Kombinationen.
Beispiel : An einen Fußballtag gibt es 9 Spiele.Es gibt 3 Ausgänge (Ereignisse)
1. Mannschaft A gewinnt
2. Mannschaft B gewinnt
3. Es gibt ein Unentschieden
eingesetzt n1=n2=n3=n= 3 = konstant mit k Spiele (Anzahl der Spiele)
3 * 3* 3*3*3.....= 3^9=19683 Mögliche Kombinationen
Wichtig : Die Ereignisse n1 und n2 und n3 müssen unabhängig sein !
n2 darf nicht abhängig von n2 oder n3 ... sein
QUELLE : "Mathematik" Analytische Geometrie/Stochastik Band 2 mit Lösungsbuch , Cornelsen Verlag
Kosten 45 Euro
TIPP : Besorge dir diese Bücher.Da sind viele Beispiele aufgeführt.
Hier das Baumdiagramm
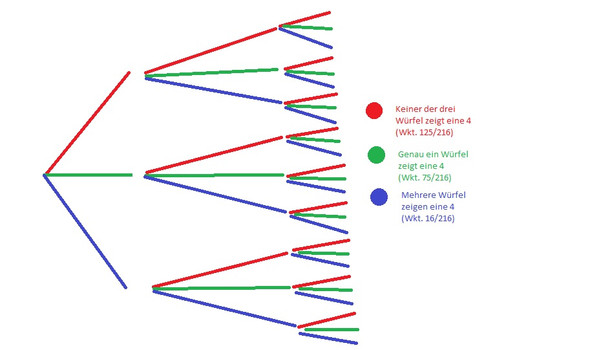
Du meinst folgendes:?
Z.B.
Eine Schale enthält 5 Kugeln, davon sind 3 blau und 2 gelb...
Wie hoch ist die Wahrscheinlichkeit, dass man bei 2x ziehen nur gelbe Kugeln zieht?
Da weiß ich natürlich, dass man die Wahrscheinlichkeiten für die Versuche multiplizieren würde. :)
Nur teilweise gibt es ja auch Aufgaben, bei denen man noch mehrere Ergebnisse dieser Mulitplikationen addieren muss, wofür mir aus dem Kopf gerade leider kein Beispiel einfällt und bei denen habe ich noch Probleme. ;)
Hoffe das war einigermaßen verständlich und danke schon mal für deine Antwort! :)