Technische Mechanik: Auflagerreaktionen bestimmen/berechnen ?
Hallo,
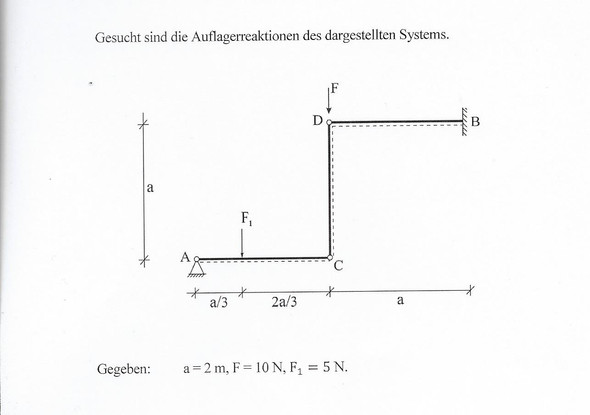
in TM haben wir folgende Aufgabe (s.Bild) bekommen zu Auflagereaktionen. meine erste frage ist, wenn ich nur die drei gleichungen nach der horizontalen, vertikalen und dem moment schreibe, sind da noch zu viele unbekannte. das heißt ich habe dann das system in zwei teilsysteme geteilt und zwar dort wo die beiden gelenke verlaufen und den drehpunkt dort bei G sozusagen dann gesetzt. ist das so richtig? trotzdem weiß ich nicht wie ich die genaue Zahl von Ax und Bx bestimmen soll, oder reicht einfach Ax=-Bx??
kann mir jemand bisschen bei der herangehensweise helfen? ich weiß ja so grob wie es geht, aber so alles noch nicht.. und wie ist das mit dem Moment bei der Einspannung oben rechts?
Vielen Dank im Voraus :)
3 Antworten
Also ganz Streng genommen, sollte es möglich sein, genug Gleichungen aufzustellen, um ein Gleichungssystem zu lösen.
Du hast 5 Unbekannte (Av und Ah, sowie Bh, Bv und das Einspannmoment in B). Dazu braucht man nur 5 Gleichungen.
Summe V = 0
Summe H = 0
Und dann noch 3 mal die Momentensumme, wobei sich die Momentensumme und die Punkte A, C und D anbietet, denn hier gilt M = 0
Wie du aber schon richtig sagst, kann man das System zerlegen und muss dann nicht 5 Gleichungen mit 5 Unbekannten auflösen.
Wenn man ein System zerlegen will, muss man immer einen Teil entfernen, sodass der Rest für sich Standsicher ist. Der Weggenommene Teil, hängt dann am Rest.
In diesem Fall sind dann offenbar die Stäbe AC und CD die weggenommen werden müssen, der Kragarm steht für sich allein.
Der Stab CD kann hierbei sofort als Pendelstab erkannt werden: keine Last auf ihm und an den Enden Gelenke. Dieser Stab hat also nur eine Normalkraft, was in diesem System eine Vertikalkraft ist.
Damit reduziert sich Stab AC zu einem Balken auf 2 Stützen mit Einzellast im Drittelspunkt. Eine sehr einfaches System, die Auflagerkräfte sind schnell als Verhältnisgleichung ermittelt:
Av = 3,333 N
Womit aus Summe V = 0, Bv zu 11,67 kN ermittelt werden kann.
Ah = Bh = 0, folgt als der Kopplung mittels Pendelstab.
Womit aus Summe M um B, das Einspannmoment B mit 23,333 Nm ermittelt wird.
Alternativ hätte man natürlich auch gleich sehen können das Ah = Bh = 0 gilt und nur mehr 3 Unbekannte gehabt, und 3 Gleichungen.
Aber ein Gleichungssystem mit 3 Unbekannten ist noch immer aufwendiger als die weitere Zerlegung.
Du könntest es auch ohne Zerlegung machen, aber dann läuft es auf ein Gleichungssystem hinaus.
Sinniger ist aus meiner Sicht den Stab AC sofort als Balken auf 2 Stützen mit Einzellast zu berechnen, dann löst sich der Rest des Aufgabe in Wohlgefallen auf.
Die Schwierigkeit besteht eigentlich darin, soviel Erfahrung zu haben, dass man den Balken auf 2 Stützen schnell erkennt.
Gerne, noch ne Frage, muss nicht Av gleich -Bv sein, ich kriege dieselben ergebnisse überall, außer bei Av. :/ weil ich hab zuerst nicht zerlegt und das gesamtsystem betrachtet, da sind ja Av und Bv die einzigen vertikalen kräfte und das gleich null, wenn man das jetzt umstellt ist doch Av=-Bv oder?
nein Ah und Bh müssen gleich sein, weil es ja keine äußere Horizontallast gibt.
Aber Bv und Av können unterschiedlich sein, hier gilt nur
Bv + Av + F + F1 = Summe Vertikaler Kräfte = 0
Das kann man sich leicht vorstellen, wenn man mal die Kräfte F und F1 direkt auf A verschieb. Diese Kräfte stehen auf dem Auflager und gehen direkt dort rein. Auflager B würde nicht bemerken ob sich diese Kräfte ändern. Auflager Av und Bv sind also nicht gleich.
ok hatte es doch rixhtig hab die komponenten nur von vornherein anders benannt.. aber wieso soll Ah und Bh gleich null sein? bei mir kommt da -35/5 bzw 35/5 N raus :/
noch eine kurze frage, weil ich gerade verwirrt bin: wenn ich den linken unteren stab alleine betrache also stab AC und das freischneide, muss ich an punkt C noch dadrüber die Kraft F die ja eig senkrecht dazu einwirkt auch mit zeichnen? oder gehört kraft F nur zu stab DB?
huhu
F gehört zu DB, weil der Stab AC ein Kraft an C nicht abtragen könnte.
Es würde aber kein Fehler entstehen wenn du die Kraft auf AC setzt, denn das Ergebnis wäre, dass die Kraft nur durch den Stab CD wieder an D zurückgehägt werden kann.
Allerdings muss man dann bei der Ermittlung der Stabkraft CD bedenken, das man die Kraft einmal nach unten geholt hat und das die danach wieder zurückgehängt wird - sich also aufhebt.
Da das dann schnell vergessen wird und man die Stabkraft CD falsch berechnet, würde ich diesen Rechenweg nicht empfehlen.
Schön dass Du Dir Gedanken gemacht hast.
Leider hat es Fehler: Punkt G ist in der ganzen Zeichnung nicht vorhanden und was meinst Du mit Ax und Bx?
Bei A gibt es keine horizontalen Kräfte und keine Momente. Dasselbe gilt für C und D. Bei B gibt es nur ein Moment und eine Vertikalkraft.
Wenn wir die Zugkraft in der Stange CD als Unbekannte annehmen, gibt es schlussendlich zwei Gleichungen mit zwei Unbekannten, nämlich die Gleichgewichtsbedingungen für AC und für BD.
Viel Erfolg!
Das Moment bei B ist einfach: (F + Fc) * a
wobei Fc = Zugkraft in der Stange CD.
(Achte auf Vorzeichen)
Du hast an Unbekannten:
- die horizontalen und vertikalen Reaktionskräfte in A, C und D (sind 6)
- die horizontale und vertikale Reaktionskraft sowie das Reaktionsmoment in B (sind 3)
An Gleichungen hast du für jeden der drei Balken jeweils das horizontale und vertikale Kräftegleichgewicht sowie das Momentengleichgewicht.
Macht 9 Gleichungen für 9 Unbekannte. Das ist normalerweise eindeutig bestimmt.
Deine Überlegung ist korrekt, aber unnötig kompliziert. Falls die Durchbiegung vernachlässigt wird, gibt es keine Horizontalkräfte und in der Stange CD keine Momente!
vielen dank, aber so wörter wie pendelstab hatten wir nicht. also kann man es auch ohne zerlegung machen? denn dort kann ich die unbekannten aber nicht so genau mit zahlen bestimmen wie du es gemacht hast..