Mathe Parabel 4.Ordnung bestimmen?
Parabel 4. Ordnung schneidet x-Acshe an A (2;0) und am Punkt B(0;2) Wie bestimme ich die Gleichung? Mit f(x) = ax^4 + bx ^2 + c aber weiter?
2 Antworten
A und B sind nullstellen. also:
f(2)=0
f(0)=0
Außerdem sind A und B punkte:
f(0)=2
und wir wissen das es in A und B keine steigung gibt:
f'(2)=0
f'(0)=0
dann einfach die bedingungen in f(x) = ax^4 + bx ^2 + c einsetzen.
bsp: f(2)=0:
f(2)=a*2^4 + b*2² + c = 0
--> ausrechnen:
16a + 4b + c = 0
sobald du alle bedingungen eingesetzt hast, löse die dadurch entstandenen in einem gleichungssystem.
gar nix. denn wir haben unsere 5 bedingungen schon. in dem fall brauchen wir sogar nur drei. außerdem haben wir f(0)=0 bereits als bedingung angegeben.
nein c kann nur eine zahl sein.
verwende nur 3 bedingungen! am leichtesten sind die, welche mit x=0. da braucht man dann nix mehr rechnen
Hallo bangboy5555,
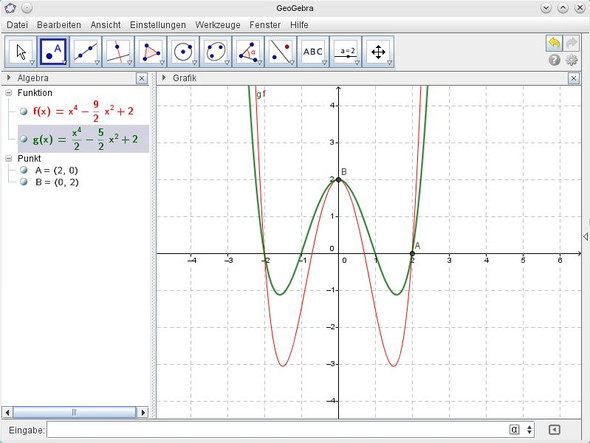
zwei mögliche Lösungen zeigt das Bild. Mit dem Ansatz y = ax^4+bx^3+cx^2+dx+e braucht man 5 Bedingungen zur Lösung der 5 Unbekannten, gegeben sind aber nur zwei Bedingungen. Mit dem Ansatz y = ax^4+cx^2+e braucht man 3 Bedingungen zur Lösung der 3 Unbekannten a,b,c. Für a habe ich a=1 gewählt. Damit ergibt sich die rote Lösung. Für a habe ich a=1/2 gewählt und erhalte die grüne Lösung. Es gibt natürlich noch unendlich viele weitere Lösungen.
Gruß von leiermann
A und B sind nullstellen. also:
f(2)=0
f(0)=0
Außerdem sind A und B punkte:
f(0)=2
Was denn nun???????????