Symmetrieebene zweier Ebenen bestimmen?
Hallo, ich habe Schwierigkeiten diese Aufgabe zu lösen.
Aufgabe:
Die Ebenen E: 3x1 + x2 - 4x3 = 8 und
F: 3x1 + x2 - 4x3 = -5 sind zueinander echt parallel.
Gebe eine Gleichung der Symmetrieebene an (d.h. Die Ebene die zu E & F den gleichen Abstand hat)
Muss man nun den Lotfußpunkt bestimmen oder wie müsste man vorgehen?
LG
2 Antworten
oder wie müsste man vorgehen?
Da beide Ebenen dieselben Koeffizienten haben, genügt es hinter dem Gleichheitszeichen zwischen 8 und -5 den Mittelwert zu bilden.
Daher Lösung:
Mittelebene G:
G: 3x1 + x2 - 4x3 = 1,5
Und hier das ganze Graphisch:
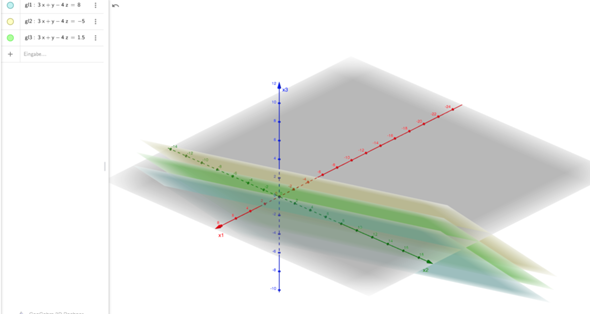
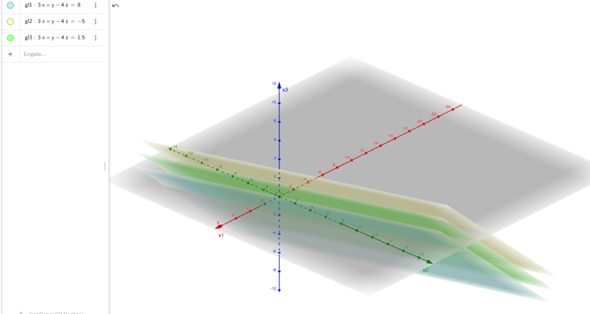
Hallo,
behalte die Koeffizienten bei und setze rechts vom Gleichheitszeichen das arithmetische Mittel zwischen 8 und -5, also 1,5.
Dann bekommst Du automatisch die Ebene, die genau zwischen den beiden liegt:
3x1+x2-4x3=1,5.
Herzliche Grüße,
Willy