Stochastik - Kugeln auf zwei Urnen verteilen?
In einer Urne sind eine schwarze und drei weiße Kugeln; in einer anderen zwei schwarze und zwei weiße Kugeln. Ein Münzwurf entscheidet darüber, aus welcher der beiden Urnen eine Kugel gezogen werden muss. Ist die gezogene Kugel schwarz, so erhält man einen Gewinn.
Nun erhält man die Erlaubnis, die 8 Kugeln vor Spielbeginn nach Belieben auf die zwei Urnen zu verteilen. Anschließend entscheidet wieder ein Münzwurf darüber, aus welcher Urne eine Kugel gezogen werden muss. Ist sie schwarz, so gewinnt man. Wie sieht die optimale Verteilung der Kugeln auf die Urnen aus?
Also die Wahrscheinlichkeit, dass Urne 1 gewählt wird ist 0,5, entsprechend: Urne 2 0,5
Es gibt x schwarze Kugeln in Urne 1 und z Kugeln insgesamt in Urne 1
Es gibt y schwarze Kugeln in Urne 2 und a Kugeln insgesamt in Urne 2
P("Schwarz") = 0,5(x/z) + 0,5(y/a)
y = 3 - x
Denn es gibt insgesamt 3 schwarze Kugeln
a = 8 - z
Es gibt ja insgesamt 8 Kugeln
P("Schwarz") = 0,5(x/z) + 0,5(y/a)
= 0,5(x/z) + 0,5(3-x/8-z)
= 0,5*((x/z)+(3-x/(8-z))
= 0,5(((8x/z)-1)/*(8-z))+(3-x/(8-z))
= 0,5*((8x/z)-2-x)/(8-z))
= 0,5*((8x/z)-2-(xz/z))/(8-z))
= 0,5*((x(8-z)-2)/z))/(8-z))
= 0,5*((x-2)/z)
Was kann ich aber jetzt hier herauslesen.... Ist der Ansatz vielleicht komplett falsch?
4 Antworten
Dein Ansatz ist korrekt, aber vermutlich irgendwo ein Rechenfehler.
Du gelangst schnell zu der Formel :
P("schwarz") = 0,5*((x/z)+(3-x/(8-z))
da fehlt noch eine Klammer und zwar muss sie so lauten:
P("schwarz") = 0,5*((x/z)+(3-x)/(8-z))
Die optimlale Verteilung ist dort wo dieser P-Wert maximal ist.
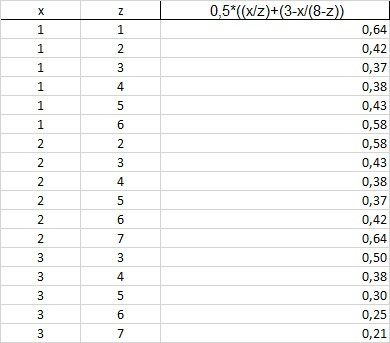
Habe ein Bild beigefügt in Excel erstellt wo alle Möglichkeiten dargestellt und berechnet sind (siehe Bild)!
Da kannst Du erkennen daß die Wahrscheinlichkeit am höchsten ist, wenn
in einer Urne 1 schwarze Kugeln allein ist und in der anderen Urne 2 schwarze und 5 weiße Kugeln, sind.
Bei Fragen zu dem Bild, stehe ich zur Verfügung!
LG,
Heni
nochmal durchgerechnet komme ich auf:
P(S) = 0,5*((x+2z)/z)
Aber hab hier auch 2 Variabeln.. Ableiten macht hier ja noch kein sinn :/
Das wäre elegant, aber im Moment sehe ich da auch nicht wie das zu machen wäre.
Ich habe eben nur für alle Varianten die Wahrscheinlichkeit berechnet!
Hab das eben nochmal berechnet, aber komme leider zu keinem vernünftigen Ergebnis :( würde es gerne auf dem rechnerischen Weg schaffen
Da wir keine weiße Kugel ziehen wollen, sollten wir diese alle zusammen in eine Urne legen. So ist die Urne ohne weiße Kugeln ein sicherer Gewinn, wenn sie beim Münzwurf ausgewählt wird.
Da es nun unerheblich ist, ob in dieser Urne 3 schwarze oder nur eine schware Kugel liegen (die Wahrscheinlichkeit eine schwarze zu ziehen liegt immer bei 100%) legen wir nur eine Kugel in diese Urne und geben die anderen 2 zu den weißen. So haben wir auch im Fall, dass die andere Urne gewählt wird, noch eine Chance von 2:5.
Wenn die Wahrscheinlichkeit, aus einer der beiden
Urnen (warum sind das eigentlich immer "Urnen"?)
zu ziehen, gleich ist, spielt die Verteilung im Grunde
keine Rolle. Es könnten auch alle Kugeln in einer Urne sein.
Stimmt nicht.
Bei der ursprünglichen Verteilung liegt die Chance für eine schwarze Kugel bei (1/2)*(1/4)+(1/2)*(1/2)=3/8
Liegt aber in einer Urne nur eine schwarze Kugel und sonst nichts, ist die Chance, diese zu erwischen, schon mal 1/2=4/8, dazu kommt noch die Chance von (1/2)*(2/7), eine der beiden anderen schwarzen Kugeln unter den fünf weißen zu ziehen.
Herzliche Grüße,
Willy
Doch, wenn man voraussetzt, dass bei dem Münzwurf
mit gleicher Wahrscheinlichkeit die eine oder die andere
Seite erscheint.
Ich finde es Logisch, alle Schwarzen in einen Behälter und alle Weißen in einen Behälter. Dann hast du eine 50% Chance eine schwarze Kugel zu erwischen. Je mehr du die Kugeln verteilst, um so niedriger wird die Chance.
Danke, muss ich dann auf was quadratisches kommen, das ich ableiten kann?