Schwerpunkt berechnen bei der Restfläche eines Viertelkreises?
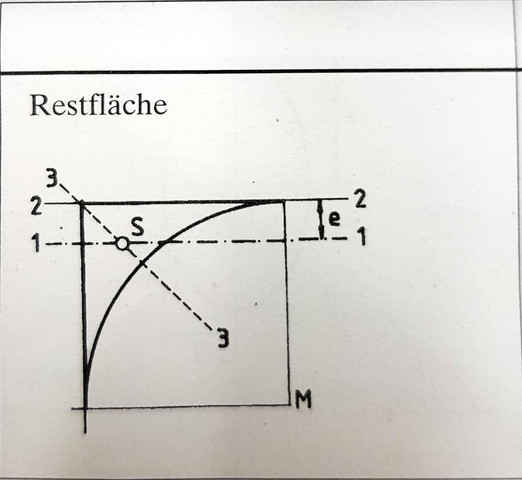
Hallo wie berechnet man die Lage des Schwerpunkts der Restfläche eines Viertelkreises, wenn der Radius gegeben ist? Auf der Skizze wäre das der Abstand e.
3 Antworten
Bei Flächenschwerpunkten kannst Du die vorhandenen Flächen in Teilflächen einteilen. Diese können dann entweder addiert oder subtrahiert werden.
Bei größeren, komplexeren Gebilden würde ich eine Tabelle empfehlen, die aber auch bei kleineren Gebilden der Übersichtlichkeit halber helfen kann.
Zunächst Teilen wir das Gebilde in zwei Flächen. Einmal das Viereck und einmal der Kreisbogen. Wir ziehen den Kreisbogen von dem Viereck ab.
Da nur Abstand e gebraucht wird, betrachten wir im folgenden nur den Schwerpunkt im Bezug auf die y-Achse.
Ich setze mein Koordinatensystem auf den Punkt M, mit links und nach oben als positiv.
In meine Tabelle gebe ich nun folgende vier Spalten:
- Fläche i
- Flächeninhalt A
- Lage des Schwerpunktkoordinate ys_i der Teilfläche
- A * ys_i
---
Fläche 1, das Viereck, hat die Maße 1mm x 1mm (nehme ich mal an, ich sehe keine Bemaßung. Wenn es eine Bemaßung irgendwo anders gibt, nehme eben die und orientiere Dich an dieser Rechnung). Damit hat 1 die Fläche A = 1 mm².
Die Lage der Schwerpunktkoordinate ys_1 ist genau in der Mitte von dem Viereck, also ys_1 = 0,5 mm.
A1 * ys_1 = 1 mm² * 0,5 mm = 0,5 mm³
---
Fläche 2, der Kreisbogen, wird abgezogen, also muss die Fläche negativ sein. Es ist ein Viertelkreis, also -A = - (1/4 * pi * r²) = - (1/4 * pi * (1mm)²) = -0,79 mm².
ys_2 = (4*r)/(3pi) = (4*1mm)/(3pi) = 0,42 mm
A2 * ys_2 = -0,79 mm² * 0,42mm = -0,3318 mm³
---
Die Formel zur Bestimmung der Schwerpunktkoordinate für die y-Achse ist jetzt:
y_s = (SUMME: ys_i * A_i) / (SUMME: A_i)
Wir brauchen also noch unsere Summen. Für (SUMME: ys_i * A_i) haben wir: 0,5mm³ - 0,3318mm³ = 0,1682mm³.
Für (SUMME: A_i): 1mm² - 0,79mm² = 0,21mm².
---
Mit der Formel rechnen wir:
y_s = 0,1682mm³ / 0,21mm² = 0,8 mm
Aber Vorsicht! Die 0,8mm gelten jetzt immer noch im Bezug auf unseren Koordinaten-Ursprung. e ist aber von oben angesetzt! D.h. e = 1mm - 0,8mm = 0,2mm
Das sollte so ungefähr stimmen mit den Maßen, die ich gewählt habe. Nur ist das Ergebnis nicht sehr genau, da ich meist sehr stark gerundet habe, aber das Prinzip sollte jetzt klar sein.
Gruß, H.
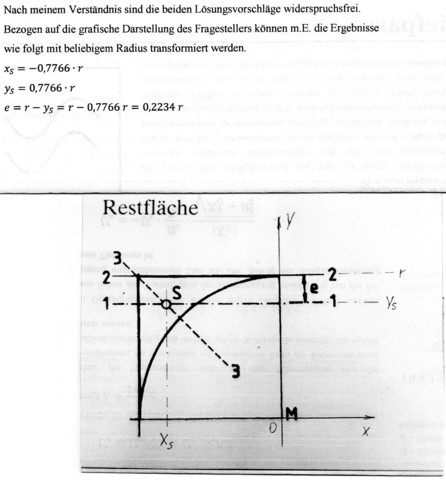
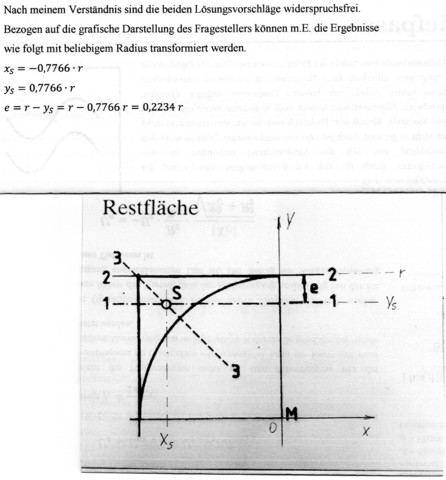
Der Eifachheit halber passen wir die Form so an, dass M der Mittelpunkt des Koordinatensystems bildet und der Radius 1 beträgt. Anschliessend spiegeln wir die Form an der y-Achse.
Die Restfläche wird begrenzt durch 0<x<1 und sqrt(1-x^2)<y<1. Da die Fläche den Inhalt 1-pi/4 hat, ergibt sich die x-Koordinate des geometrischen Schwerpunkts zu 1/(1-pi/4)*integral(x)dxdy über die genannten Grenzen. Konkret ist das 2/3*1/(4-pi)=0.7766...
Aus Symmetriegründen sind die y-Koordinate gleich.