Wie lautet der Satz von Vieta, wenn man mit kubischen Gleichungen arbeitet?
Wenn die Aufgabe beispielsweise lautet:
Finden Sie eine Polynomgleichung mit den Lösungen 1, 2 und 3.
Wie macht man das dann?
bei einer quadratischen Gleichung wäre der Satz von Vieta ja:
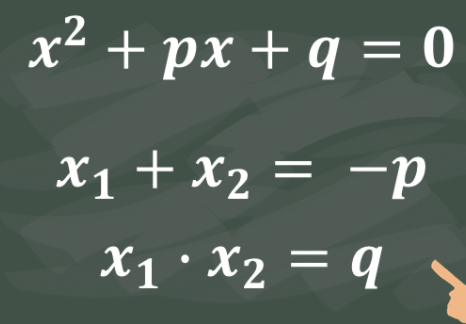
Aber wie wäre er bei kubischen gleichungen oder vielleicht sogar polynomgleichungen 4. Grades?
3 Antworten
Der Satz von Vieta ist nur ein Spezialfall.
Für die Erzeugung eines Polynoms z.B. dritten Grades mit den Nullstellen x1, x2 und x3 gilt (x - x1) * (x - x2) * (x - x3) = 0. Und dann ausmultiplizieren. Das geht auch mit höheren Graden.
Der Spezialfall Vieta:
(x - x1) * (x - x2) = 0
ausmultipliziert
x² - (x1 + x2) * x + x1 * x2 = 0
Damit ist p = -(x1 + x2) und q = x1 * x2.
also wenn man zum beispiel die aufgabe oben nimmt mit den lösungen 1, 2 und 3 ? Wie genau setzt man die dann in diese Formel ein?
x1 und x2 sind die gegebenen Nullstellen. Ziel ist es, ein Polynom x² + px + q zu konstruieren, das genau diese Nullstellen hat. x ist die Variable, p und q sind Konstanten, die die Nullstellen bestimmen.
Also ich Suche ein Polynom (eine Parabel) mit z.B. den Nullstellen 2 und 3. Dann ist x1 = 2 und x2 = 3. Das Polynom ist dann f(x) = (x - 2) * (x - 3).
Ausmultipliziert ist das f(x) = x² - 5x + 6. Diese Funktion hat genau die gewünschten Nullstellen 2 und 3.
https://www.wolframalpha.com/input/?i=x%C2%B2+-+5x+%2B+6
("Roots" sind die Nullstellen)
Wolfram Alpha ist auch so schlau, die ursprüngliche Funktion f(x) = (x - 2) * (x - 3) herauszufinden.
Für das Beispiel 1, 2 und 3 ist das f(x) = (x - 1) * (x - 2) * (x - 3) = 0
Und schrittweise ausmultiplizieren f(x) = (x² - 3x + 2) * (x - 3)
f(x) = x³ - 6x² + 11x - 6
Und sicherheitshalber Wolfram Alpha fragen
https://www.wolframalpha.com/input/?i=x%C2%B3+-+6x%C2%B2+%2B+11x+-+6
Wenn die Nullstellen z.B. -3 sein soll, steht dort (x + 3).
Der Sinn dahinter ist, dass wenn x genau die Nullstelle (hier -3) ist, dass der Klammerausdruck 0 wird und damit f(x) = 0 erzwingt. Jede Nullstelle z.B. 1, 2 und -3 bringt einen solchen Klammerausdruck mit: f(x) = (x - 1) * (x - 2) * (x + 3).
Wenn x genau diese Nullstelle (z.B. x = 2) erreicht, wird der entsprechende Faktor (z.B. (x - 2)) zu 0.
f(x) hat dann dort eine Nullstelle, weil ja mit 0 multipliziert wird.
Bei einer Funktion 4. Grades kannst du durch Substitution lösen.
x^2=z : dann hast du eine Gleichung az^2+bz+c
Am Ende noch resubstituieren.
Das funktioniert aber nur dann, wenn die Gleichung 4. Grades eine sehr spezielle Form hat, nämlich
a x^4 + b x^2 + c = 0
(das heißt, die Glieder mit x^3 und mit x^1 sind gar nicht da)
Einfach die Gleichung (x-1)(x-2)(x-3)=0 nehmen und ausmultiplizieren !
beim spezialfall von vieta für was genau steht das x, das x1 und das x2? das hab ich irgendwie noch nie so richtig verstanden