Quadratische Text Aufgabe?
Ich schreibe bald eine Klausur über die quadratische Funktionen und kann mich gar nicht mit die Text Aufgabe umgehen. Kann jemanden vielleicht mir erklären wie man diese Aufgabe lösen bitte.
2 Antworten
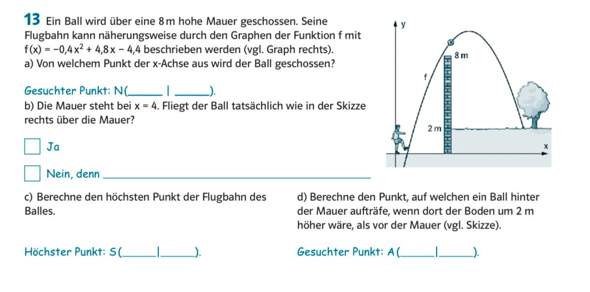
a)
Nullstellen berechnen und den kleineren Wert nutzen - der größere wäre die Stelle, wo der Ball aufkommt. Du berechnest also mittels abc-Formel (oder was ihr gelernt habt) alle x, für die –0.4x²+4.8x–4.4=0 gilt. Das wäre dann der Punkt (1|0).
b)
Berechne f(4)=–0.4•4²+4.8•4–4.4 und schau, ob die Höhe des Balls höher als die der Mauer ist. Ja, tut er.
c)
Die Ableitung f'(x)=–0.8x+4.8 gleich Null setzen, da die Steigung am höchsten Punkt null ist. Nach x umformen und die errechnete Stelle in f(x) einsetzen. Der höchste Punkt ist dann (6|10). Wenn dir der Begriff der Ableitung nicht bekannt ist, musst du einfach den Scheitelpunkt bestimmen. Diesen kannst du ablesen, wenn du f(x) in die Scheitelpunktform bringst mittels quadratischer Ergänzung.
d)
Berechene das x, für das –0.4x²+4.8x+4.4=2 gilt und nimm den größeren der beiden Werte - der kleinere liegt links von der Mauer, der größere rechts von ihr. Das ist dann der Punkt (–2√(5)+6|2).
Bittesehr :)
Erkennst du, was gefragt ist und/oder benötigst du Hilfe bei der Rechnung?
a)
Der Ball wird auf der x-Achse abgeschossen, auf Höhe 0.
Du musst die Nullstelle berechnen f(x) = 0.
Es gibt zwei Nullstellen. Übeleg dir, welche Nullstelle gefragt ist.
b) Die Mauer ist 8 m hoch. Prüfe, ob bei x = 4 der Funktionswert größer als 8 ist,
f(4) > 8
c) Scheitelpunkt bestimmen.
d) Hier musst du ausrechnen, wo der Funktionswert 2 ist, f(x) = 2.
Du bekommst zwei x-Werte. Das der Ball hinter der Mauer auftrifft, überleg dir, welcher x-Wert der richtige ist.