Profi-Taschenrechner mit sehr vielen stellen
hallo,ich suche einen taschenrechner, mit dem ich ein paar tausend stellen rechnen kann. u.a. brauch ich das ergebniss von 11^2004 danke shcon mal.
lg
7 Antworten
Das Ergebnis ist: 89318425157349529897524029811641001572580563919094656904500892985608066414191555820853297110939698354814802206102031442460753211637120451524994092236085895721295158417163918670364080438313689830192908261851253985369763528461540542783842727093046220485126646504003602563278805434571231366832941862025167098752604905475762250985209909602811754208501278557357107002677485333927595931070649045905314428383113153840856121789635062407713660017201043736980202443099264641253735120889884013397529720069629692628827460526353608432614305060671195020080030537603143665237006394432862276411572182816744754360004866065300946065792467004266787893063905072471508156873882181958932311607495412691809319943631541120093388716372784607218367156598953644138328878844248806816784996068399187118267055449055402715167283520055702527587305907175638888539346383819780264270030646721204372901764106292063517576945919446348080626220157461893042053686955003851131891796399677589004608635921617916898347610989958843203330833701294923720070965443569823080867404379544605098145064984204123663997384066903510236470873287488424767002706066325619320150254450561497023259421747263520959440406248677125243482518844240428859890002437812420107053991003344632985333329920780374138741714994033066725261949767824319047967230044117419717693597276315283279769917224688408343612913940136511485083237258261651974892873370782756618827908400323191178921419377299846368054742643357729880313451056918738506205895029520437344494463247835563233221950397677537832862105282818660244049953092574001324475832170389104913959665579785560449735114026933685674970969455383315908025056179292874915701870155857687414720285590648849808169959571373119060364971328568925823466015739653726567718833570528168670202995145054949422881397944130019127124653456497575807383574204509394104187532347833116951680955412673744264097446479862550426917335884802951009867779819543828145181790751430148490406668508127453605240965717347451163417070727295025626930940925997200364547352547646050086382150964792679387231011879909537350021897733875473830124958573557734641
sind 2005 Stellen, das macht ein Bildschirm noch, ein Taschenrechner allerdings nicht mehr.
Die als größte praktisch zu erwartende Zahl wurde mal mit 10^100 = 1 Googol (daher Google) angenommen. Theoretisch gibts keine Obergrenze, aber die 10^100 dürfte über der Zahl der Teilchen im Weltall geschätzt (um 1970 mit den damaligen, endlichen Weltmodellen warens so ca. 10^50) liegen.
10^2004 hat keinen realen Nährwert! Und ein Taschen(!)rechner, der sowas kann, ist nicht nachgefragt. Wenn er die Zahl genau rechnen sollte, bräuchte er so viele bits Speicher, dass das All damit gefüllt wäre! In normaler Genauigkeit mit Exponentialschreibweise würde aber die übliche Darstellung reichen. Braucht bloß wirklich keiner, der was ernst zu nehmendes rechnen möchte!
im übrigen lassen sich sehr lange Zahlen angeblich mit Python rechnen bzw programmieren, ich kanns aber nicht.
11^2004? Willst du das als komplette Zahl ausgeschrieben haben? Das Problem ist da nicht die Rechenleistung des Taschenrechners sondern die Größe des Displays.Sowas kann man höchstens als Potenz angeben, also x*10^y
Die Anwort ist übrigens ungefähr 8,93*10^2086. Und eine Zahl mit über zweitausend Stellen schreibt wohl niemand gern auf. Und es hat auch keinen Sinn.
Und was genau bringt es dir nun die letzten beiden Ziffern einer Zahl mit tausenden von Ziffern (und das ist nichtmal übertrieben) zu wissen? Die letzten beiden Ziffern? Das sind doch die unwichtigsten Ziffern von allen, sofern man bei über 2000 Ziffern noch von wichtig und unwichtig reden kann. Das einzig sinnvolle bei so einer großen Zahl ist einfach die Angabe in einer (Zehner)potenz, in dem Fall also ungefähr 8,93*10^2.086. Meinetwegen noch ein paar mehr Ziffern nach dem Komma, aber alles andere ist schlichtweg übertrieben.
naja, es ist einnfach nur ein kleines mathe-rätsel!
Das kannst Du mit C++ selber programmieren.Aber nicht als Long sondern als kaufmännische Zahl.
Einen Taschenrechner dazu gibt es nicht.
Die höchste im normalen Rechenwesen benutzte Zahl ist ein Gogool das ist 10 hoch 100.
Damit soll man alle Atome unseres Sonnensystems einzeln nummerieren können.
Alles weitere ist Theorie.
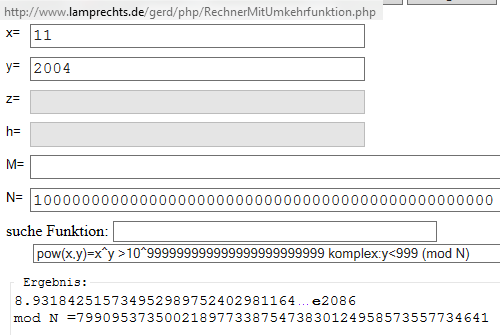
Der Rechner unter
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
kann bei pow(x,y) nicht nur sehr große Zahlen potenzieren, sondern auch die letzten 50 Stellen per Modulo Funktion:
pow(11,2004) mod (N=100000000000000000000000000000000000000000000000)
mod N =79909537350021897733875473830124958573557734641
siehe Bild
11^0 = 01
11^1 = 11
11^2 = 121
11^3 = 1331
11^4 = 14641
11^5 = 161051
11^6 = 1771561
11^10 = ...01
Schau Dir mal die letzten 2 Ziffern an und erkläre was Dir auffällt. Dann könntest Du überlegen was
11^2004 wohl für 2 letzte Ziffern haben könnte.
Da sich die endziffern regelmäßig wiederholen, und zwar alle 10 Zahlen wieder. muss 11^2004 auf 41 enden.