Minimale/maximale und mittlere Änderungsrate?
Ich habe bereits im Internet versucht zu erlesen, wie man diese berechnet, aber irgendwie war das überall anders und ich bin einfach nur noch verwirrt.
Was bedeuten diese Ausdrücke denn überhaupt ?
Ich hab gelesen, dass die mittlere Änderungsrate der Differenzenquotient also (f (x1)-f (x2)) / x1-x2 ? Stimmt das ? Und nur für die lokale Änderungsrate muss ich meine Funktion ableiten ? Ausserdem hab ich gesehen, dass es Menschen gab, die für x in die erste Ableitung den Differenzenquotient eingesetzt haben 0.0 ist das richtig ? Ist die momentane Änderungsrate die lokale Änderungsrate? Und was ist eine minimale oder maximale Änderungsrate ? Wie berechne ich die ? Sagt mit eine Änderungsrate immer aus wie stark die Steigung ist in einem Punkt ? Und brauch ich für die Steigung nicht immer die Ableitung einer Funktion ? Und unter welchen Bedingungen muss ich die zweite Ableitung 0 setzen und den bekommenen x Wert dann in die 2. Ableitung einsetzen ? Ist das nicht auch eine Steigung ?
Wie ihr seht, habe ich Unmengen an fragen. Es wäre super, wenn mir irgendwer alles ganz genau erklären könnte.
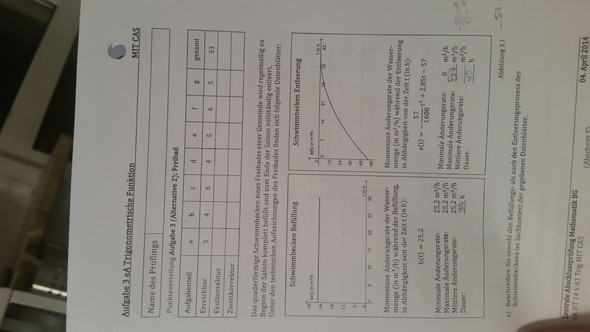
Ich habe noch eine Aufgabe, die ich lösen müsste, könnte mir dazu jemand die Lösungen geben?:)
Vielen dank :)
1 Antwort
Mit dem Differenzenquotienten ermittelst Du die durchschnittliche Steigung zwischen den zwei Punkten P1(x1|y1) und P2(x2|y2).
Bei allen Funktionen außer den linearen (das sind ja Geraden mit konstanter Steigung) ändert sich die Steigung in jedem Punkt in Abhängigkeit von x. Verbindest Du nun P1 und P2 auf direktem Weg, kannst Du mit dem Steigungsdreieck ausrechnen (y-Differenz durch x-Differenz = Differenzenquotient), wie die Steigung "aller Punkte" dazwischen im Durchschnitt ist (zwischendurch ist sie mal kleiner und mal größer).
Mit momentaner Änderungsrate ist die Steigung in einem Punkt x gemeint, also f'(x). Musst Du also die Steigung an der Stelle x0 ermitteln, setzt Du einfach x0 in die Ableitungsfunktion ein; rechnest also f'(x0) aus.
Minimale Änderungsrate ist halt die kleinste Änderungsrate (Steigung) der Funktion, also kleinstenfalls Null. Die maximale Änderungsrate hast Du da, wo die Ableitungsfunktion ihre Extremstelle hat, also bei f''(x). D. h. im Wendepunkt hat eine Funktion ihre maximale Änderungsrate (die kann natürlich positiv oder negativ sein). Mit Änderungsrate ist nämlich der "Betrag" der Steigung gemeint. Hast Du also z. B. die Steigungen [f'(x)] von -13, 0 und 10 ermittelt, dann ist -13 die maximale Änderungsrate (obwohl -13 ja kleiner ist als 10, aber die Änderung in diesem Punkt zum unmittelbar nächsten ist größer als an der Stelle, wo die Steigung 10 ist...).
Mit der zweiten Ableitung berechnest Du quasi die Steigung der Ableitung. So wie Du die Ableitung einer Funktion Null setzt, um deren Extrempunkte zu ermitteln (f'(x)=0), so setzt Du die "Ableitung der Ableitung" Null (f''(x)=0), um die extremsten Steigungen der Funktion zu ermitteln. Und das ist nun mal eine Bedingung um an die (möglichen) Wendestellen einer Funktion zu kommen.