Mathematik?

Hey

weiß jemand wie man das ausrechnet?

Answer 1

[mihisu]

Ich würde so vorgehen...

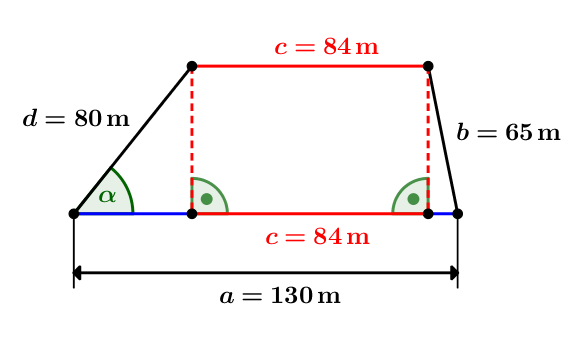
[Die Skizze ist, wie die Skizze in der Aufgabenstellung, nicht maßstabsgetreu.]

Verkürze das Trapez durch Entfernen der roten Strecken auf ein Dreieck...

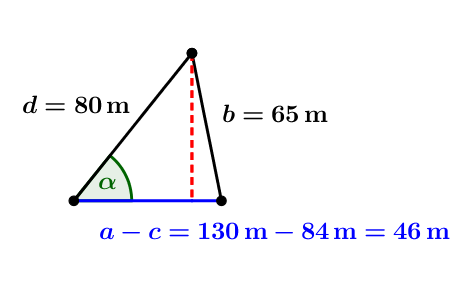
Nun hat man ein Dreieck, bei dem man mit Hilfe des Kosinussatz den gesuchten Winkel α bestimmen kann...

$b^2=d^2+\left(a-c\right)^2-2\cdot d\cdot \left(a-c\right)\cdot\cos(\alpha)$

[Addiere 2 ⋅ d ⋅ (a - c) ⋅ cos(α) und subtrahiere b².]

$\rightarrow\quad 2\cdot d\cdot \left(a-c\right)\cdot\cos(\alpha)=d^2+\left(a-c\right)^2-b^2$

[Dividiere durch 2 ⋅ d ⋅ (a - c).]

$\rightarrow\quad \cos(\alpha)=\frac{d^2+\left(a-c\right)^2-b^2}{2\cdot d\cdot \left(a-c\right)}$

$\rightarrow\quad \alpha=\arccos\left(\frac{d^2+\left(a-c\right)^2-b^2}{2\cdot d\cdot \left(a-c\right)}\right)$

$\rightarrow\quad \alpha=\arccos\left(\frac{\left(80\,\text{m}\right)^2+\left(130\,\text{m}-84\,\text{m}\right)^2-\left(65\,\text{m}\right)^2}{2\cdot 80\,\text{m}\cdot \left(130\,\text{m}-84\,\text{m}\right)}\right)$

$\rightarrow\quad \alpha\approx \arccos\left(0\text{,}58302\right)\approx \underline{\underline{54\text{,}34\degree}}$

Comments

[WhiteDragon3564]

vielen dank

Answer 2

[Willy1729]

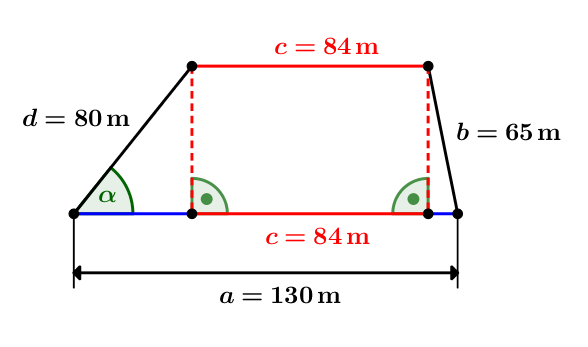
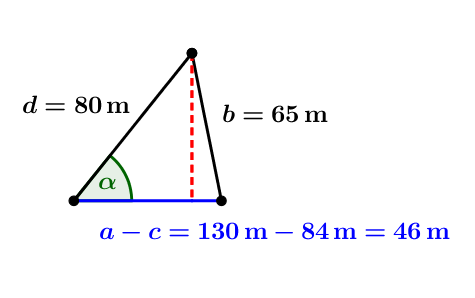
Hallo,

lege eine Parallele zu b oben an Seite d an, die Seite a in Punkt E schneidet.

Dann entsteht rechts davon ein Parallelogramm, dessen Grundseite gleich Seite c ist.

Ziehst Du c von a ab, bleibt die Strecke AE (A sei der Scheitelpunkt des gesuchten Winkels) übrig, also 46 m.

Nun hast Du drei Seiten dieses Dreiecks und kannst den Kosinussatz anwenden, um alpha zu berechnen.

Herzliche Grüße,

Willy

Comments

[WhiteDragon3564]

genau so hab ich es, aber das wäre ja der kosinussatz: b^2 = x^2 + d^2 - 2xd * cos(alpha) x... 46m und umgeformt: cos(alpha) = b^2/(x^2+d^2-2*x*d) und dann noch arccosinus(alpha), jedoch kommt dann error.

[Willy1729]

@WhiteDragon3564

Kosinussatz: a²+b²-2ab*cos (gamma)=c².

Umgeformt nach cos (gamma):

cos (gamma)=(a²+b²-c²)/(2ab).

Winkel gamma ist dann der Arkuskosinus des Ergebnisses.

Wenn Du es richtig machst, bekommst Du das Ergebnis von mihisu.