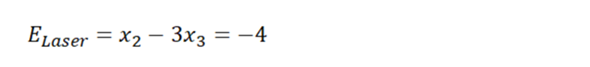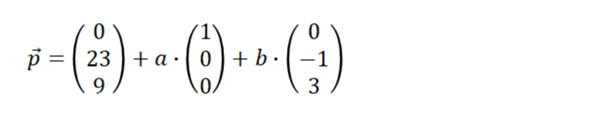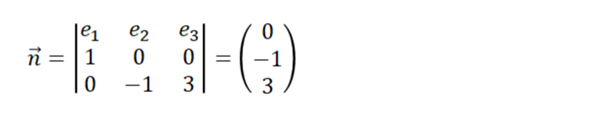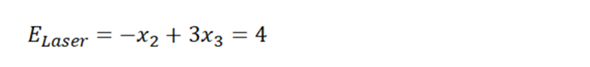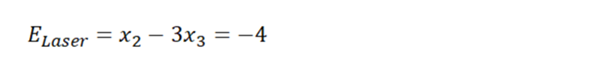Denkt ihr, dass solche Aufgaben im Abitur für den Mathe-Leistungskurs überhaupt drankommen und weiß jemand wie ich die Aufgabe löse?
Hallo,
ich schreibe in 2 Wochen mein Abitur für den Leistungskurs in Mathe und bin bei der Aufgabe einer alten Klausur einfach Planlos. Denkt ihr das kommt im Abitur überhaupt dran und weiß jemand wie ich die Aufgabe löse?

1 Antwort
Die Aufgabe ist nicht schwer, wenn man sieht, dass darin ein Klassiker der Vektorgeometrie versteckt ist. Die Umwandlung einer Ebenengleichung in Parameterform in die Koordinatenform.
Der Stützvektor der Ebenengleichung ist der Projektorort.

Und die Form der Strahlungscharakteristik

lässt sich zusammen mit dem Stützvektor in folgende Parametergleichung umformen.
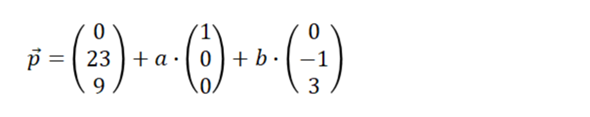
Man erkennt die beiden aufspannenden Vektoren (1 | 0 | 0) und (0 | -1 | 3). Das Vektorprodukt beider Vektoren bildet einen Normalenvektor der Ebene.
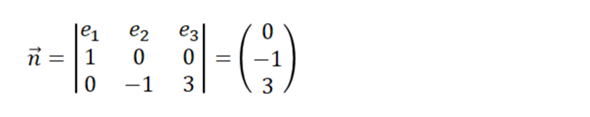
der auch gleich die Koeffizienten der Ebenengleichung in Koordinatenform liefert.

Freilich mit der zunächst unbekannten Konstante k, die sich mit einer beliebigen Koordinate aus der Parameterform bestimmen lässt. Mit a=0 und b=0 kann man einfach den Stützvektor einsetzen und erhält.

mit k=4 erhält man die Gleichung:
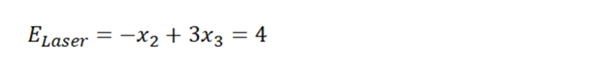
Manche stören sich daran, dass eine Gleichung mit einem Minuszeichen beginnt. Also für die Ästhetiker unter uns: