Mathe-Heron-Algorithmus?
Hallo Leute,
Und zwar verstehe ich die Aufgabe Nr. 1 nicht wirklich, ich hab wie ihr sehen könnt die Rechtecke gezeichnet nur bei 19 wusste ich nicht welchen Maß ich nehmen soll, ansonsten was ich nicht verstehe ist diese Tabelle auszufüllen, ich weiß nicht ob das so kompliziert ist, aber mein Gehirn wusste ab da nicht weiter, ich denke das ich die Erklärung von dem Lehrer nicht so gut verstanden hab, obwohl ich ich am anfang zu den Reelen Zahlen sehr gut vorbereitet was hat mich dieser Heron-Algorithmus durcheinander gebracht, jedenfalls würde ich mich sehr über eure Hilfe und wenn ihr anhand Aufgabe c) ein Beispiel geben könntet wäre super nett.


Hier ist die Aufgabe und meine Unterlagen abgebildet:)
2 Antworten
Du solltest für jede Teilaufgabe ungefähr 3 Folgenelemente ausrechnen.
Mit jedem Folgenelement zeichnest du ein Rechteck, dessen Breite der Wert des Folgenelements ist, die Höhe ergibt sich als Quotient von Radikand und Folgenelement. Aus der Zeichnung sollte erkennbar werden, dass die Rechtecke auf ein Quadrat zulaufen, dessen Seitenlänge gerade der Wert der Wurzel ist.
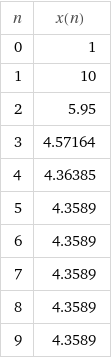
Aufgabe c: Du sollst als Startwert einen Teiler des Radikanden nehmen. Da 19 eine Primzahl ist, bleiben dir als Startwerte nur die Teiler 1 und 19, die beide gut verwendbar sind. Wenn du 19 als Startwert wählst, sind die Werte der ersten sechs Folgenelemente und der zugehören Höhen der Rechtecke (hier mit einem kleinen Programm gerechnet):
x-Wert y-Wert (19/x)
19,0 1,0
10.0 1.9
5.95 3.1932773109243695
4.571638655462185 4.156059004641331
4.363848830051758 4.353954671654987
4.358901750853372 4.358896136229784
Mit diesen Werten könntest du sogar sechs Rechtecke zeichnen. Es würde genügen, die drei ersten Rechtecke zu zeichnen. Aus den Zahlenwerten lesen wir ab, dass das 6. Rechteck in der Zeichnung bereits als Quadrat erscheinen würde, und das 5 Rechteck vom 6. Rechteck fast nicht zu unterscheiden wäre.
19=1•19=2•9,5=5•3,8
🤓