Mathe Beweis das 2^n >= n^2 ist?
Hallo,
ich hab eine Aufgabe in der ich beweisen soll das 2^n >= n^2 mit einzigster Ausnahme n = 3 für n Element von N ist. Eigentlich geht es dabei um vollständige Infuktion ich kann mir aber nicht vorstellen das dies hier funktioniert. Jetzt wollte ich die Schnittpunkte der Funktionen ausrechnen um zu untersuchen ob 3 darunter liegt dies ist aber auch nicht ohne Taschenrechner möglich.
Wär nett wenn ihr mir helfen könntet.
6 Antworten
Hallo,
wenn für n>=4 gilt, daß 2^n>=n² ist, dann muß bewiesen werden,
daß 2^(n+1)>=(n+1)² ist
2^(n+1)=2*2^n
(n+1)²=n²+2n+1
2*2^n ist das Doppelte von 2^n.
Das ist größer oder gleich n²+2n+1, wenn dies nicht mehr als das Doppelte von n² ist. n² muß also größer oder gleich 2n+1 sein für alle n >=4.
Hier kannst Du noch einmal mit der vollständigen Induktion einsetzen.
Für n=4 stimmt die Behauptung: 16>=9
Dann muß gelten: (n+1)²>=2n+3
n²+2n+1>=2n+3
Die rechte Seite der Gleichung ist nur um 2 größer als 2n+1. Dafür kommt auf der linken Seite aber n² als Summand hinzu, der für n>=4 immer höher als 2 ist.
Damit ist n² für alle n>=4 größer oder gleich 2n+1. n²+2n+1 kann also nicht mehr als doppelt so groß wie n² werden. 2*2^n ist also für alle n>=4 immer größer oder gleich n²+2n+1
Herzliche Grüße,
Willy
(IA) Sei n = 4, dann 2^4 = 16 >= 16 = 4^2.
(IS) 2^(n+1) = 2*2^n = [IV] 2(n^2) = n^2 + n^2 >= n^2 + 2n +1 = (n+1)^2.
Einzige Sache die du noch per Hand zu zeigen hast: n^2 >= 2n + 1, wenn n >= 3. Da genau diese 3 kleiner als der Induktionsanfang (4) ist, funktioniert der Induktionsschritt auch immer, das sollte man anmerken.
LG
Du meinst wohl bis auf n = 2
Ich habe dir mal die Graphen gezeichnet. Hoffe es hilft dir weiter.
In der Darstellung wurde n durch x ersetzt.
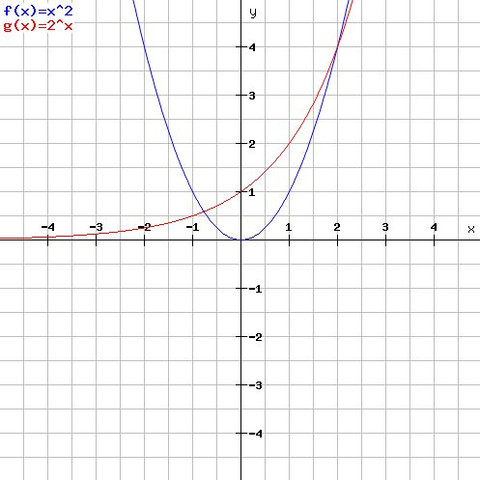
Stimmt, du hast Recht! Das hatte ich nicht richtig gelesen - sorry ;) Aber grafisch ist es manchmal einfacher :D
Der beste Beweis ist in der Tat durch Induktion. Wenn ich dir jetzt die Lösung präsentiere, dann kann ich aus langjähriger Erfahrung als Tutor sagen, dass die Studenten/Schüler, die diese Aufgabe nicht selber lösen zu hoher Wahrscheinlichkeit in der Prüfung durchfallen oder knapp mit einer sehr schlechten Note bestehen. Daher gebe ich dir nur einen Tipp und rate Dir es dann selbstständig, oder noch besser in einer Gruppe zu lösen.
Tipp: Induktionsanfang ist n = 4
Das hab ich bereits versucht das Problem ist nur das ich dann für die induktion auf eine Ungleichung der Form 2*2^n >= n^2 + 2n + 1 komme da ich aber ne Ungleichung habe kann ich ja nur sagen das 2^n >= n^2 ist. Wie kann ich da jetzt irgendwie was rauslesen. Ich mach das übrigens eh nur weil ich Lust hab studier leider noch kein Mathe :(
Ah ok. Wenn du schon soweit bist, dann hier der nächste Tipp: Du musst irgendwie hinkriegen von 2*2^n nach n^2 + 2n + 1 zu kommen.
Ich mache schonmal den ersten Schritt:
2 * 2^n >= 2 * n^2 (nach Induktionsvoraussetzung: 2^n >= n^2)
Du siehst ich konnte 2^n einfach durch n^2 ersetzen, denn somit ist die Ungleichung 2 * 2^n >= 2 * n^2 immer noch erfüllt. So ab hier musst du immer weiter nach unten abschätzen bist du n^2 + 2n + 1 erreicht hast.
Mir scheint, dass du eventuell die Bedeutung der Induktion und der unteren Abschätzung noch nicht ganz verstanden hast, daher hier nochmal ein kleines Beispiel:
Wir wollen zeigen, dass 2^n >= n^2 gilt. Wie du bereits richtig erkannt hast, gilt dies nicht für n=3 aber ab n=4. In anderen Worten ab n=4 ist die Ungleichung 2^n >= n^2 IMMER richtig, aber das müssen wir noch formal beweisen. Also daher A(n) => A(n+1), also für jede natürlich Zahl n > 4.
Also wir wollen zeigen, dass 2^(n+1) >= (n+1)^2 ist. Nur können wir dies hier nicht auf direktem Wege, sondern müssen eine "Kette" von Ungleichungen bilden, ungefähr die so aussieht:
2^(n+1) = 2 * 2^n >= aaaaa >= bbbbb >= ...... >= xxxxx >= n^2 + 2n + 1 = (n+1)^2.
Im ersten Schritt habe ich dir bereits durch Induktionsvoraussetzung gezeigt:
2^(n+1) = 2 * 2^n >= 2 * n^2 >= bbbbb >= ..... >= xxxxx >= n^2 + 2n + 1 = (n+1)^2
Jetzt musst du nur noch die Kette vervollständigen. Tipp nebenbei: Die Kette ist sehr kurz ;-)
Ach shit. Sehe gerade, dass dies schon die Lösung ist.....Ich verfluche meine Übereifrigkeit. Aber du kannst ja überlegen warum das so ist.
Für die Fälle n=1, n=2 und n=3 musst du übrigens jeweils einzeln nochmal zeigen, sonst ist der Induktionsanfang mit n=4 unvollständig
Warte mal das versteh ich nicht...
n=3
2³ = 8
3² = 9
2^n <> n^2
Es muss aber gelten 2^n >= n^2. Mit n=3 ist aber 8<9, und somit ist die Relation nicht erfüllt
n=3 als Ausnahme stimmt schon:
2³=8, 3²=9
Hier stimmt die Behauptung also nicht, daß 2^n größer oder gleich n² ist. Für n=1 stimmt sie: 2^1>1², für n=2 stimmt sie auch:
2²=2²